Se um projétil é disparado da origem do sistema de coordenadas com uma velocidade inicial , em uma direção que faz um ângulo o com a horizontal, calcule o tempo necessário para que o projétil cruze uma linha que passa pela origem e faz um ângulo com a horizontal.
Passo 1
Fala, galerinha. Estamos aqui pra mais um exercício, mas calma que vou te ajudar nessa.
Segue a imagem pra entendermos melhor o que está sendo feito.
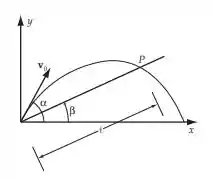
Nessa questão temos um projétil que está sendo lançado na direção que faz um ângulo com a horizontal e queremos o tempo para ele passar a linha que faz um ângulo com a horizontal. Novamente, temos que ver os movimentos nos eixos que temos. Vamos aos cálculos.
Passo 2
Começamos analisando o movimento no eixo e . Como é comum nesse tipo de exercício, temos um movimento constante no eixo e um acelerado com a aceleração sendo a gravidade pra baixo. Assim, separamos os movimentos, temos
No eixo
Como a força é zero nessa direção, temos . Assim, a equação da velocidade vai ficar
Integrando essa equação no tempo, temos
Já no eixo temos
Como a força nessa direção é a força gravitacional, vamos ter que . Então nossa equação de movimento fica
Integrando essa equação em relação ao tempo, temos
Integrando novamente em relação ao tempo
Passo 3
Agora vendo as coordenadas do ponto P atingido são
No eixo
No eixo
Igualando essas coordenadas desses pontos as equações de movimento que temos
Substituindo o tempo gasto para atingir o ponto P e isolando na primeira equação e substituindo na segunda, vamos obter
Dessa equação obtemos que , que é a solução que não nos interessa, ou
Resposta
Mais um problema feito. Bora pra mais um?