Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.7 - Ex. 149
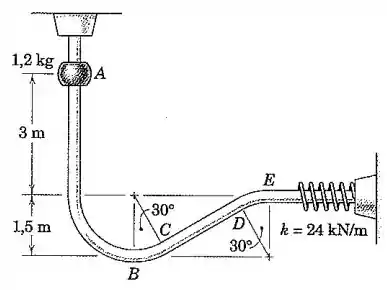
O cursor de é liberado a partir do repouso na posição e desliza sem atrito ao longo da guia no plano vertical mostrada. Determine
(a) a velocidade do cursor quando este passa a posição e
(b) a deflexão máxima da mola.
Passo 1
(a) Nesse caso, como não há atrito, a energia mecânica do sistema se conserva. Vamos considerar a altura de como a altura zero do sistema, beleza?
Passo 2
(b) Na máxima compressão da mola, onde consideraremos ponto , a energia cinética se anula:
Resposta
(a)
(b)
Exercícios de Livros Relacionados
A transmissão por fluido de um caminhão de 15000 kg permite que o motor forneça potencia constante para as rodas traseiras. Determine a distancia necessária para o caminhão, rodando em uma estrada pla
O carrinho de mina de 1,2 Mg está sendo puxado pelo guincho M montado no carrinho. Se o guincho gera uma potencia de saida constante de 30Kw. Determine a velocidade do carrinho no instante em que ele
O elevador de carga e a carga tem uma massa total de 800kg, e o contrapeso C tem massa de 150kg. Se a velocidade para cima do elevador aumenta uniformementede 0,5 m/s para 1,5m/s em 1,5s, determine a
Determine a velocidade da caixa de 100 kg após 15 s se o motor opera com uma eficiência de ( ε ) =0,8. Se a potencia de entrada do motor é de 2kW. O coeficiente de atrito cinético entre a caixa e o pl
Se o motor de um carro de 1,5 Mg gera uma potencia constante de 15kW, determine a velocidade do carro após ele ter se deslocado uma distancia de 200 m em uma estrada plana partindo do repouso. Desprez