Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 29a

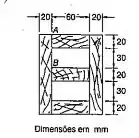
Várias pranchas são coladas juntas para formar a caixa mostrada. Sabendo-se que a viga é submetida a uma força cortante vertical de 3kN, determine a tensão de cisalhamento média na junta colada: (a) em A;

Passo 1

Precisamos calcular o momento de inércia, nesse caso as duas peças laterais tem centros coincidentes com o da peça. Para as peças de cima e de baixo vamos aplicar o teorema dos eixos paralelos.

I 1 =   20 × 120 3 12 = 2,88 × 10 6 m m 4

Pelo teorema dos eixos paralelos temos:

I = I 2 + A d ²

Onde d é a distância do centro do sistema ao centro da peça de baixo ou de cima e vale 50mm.

As peças de cima e de baixo tem dimensões:

b = 60 m m

h = 20 m m

I = 60 × 20 3 12 + 60 × 20 × 50 ²

I = 3,04 × 10 6 m m 4

I t o t a l = 2 I 1 + 2 I =   11,84 × 10 6 m m 4

Passo 2

Precisamos calcular o momento estático para encontrar o fluxo, pro ponto A o momento estático que nos interessa é da peça a direita da ligação em cima:

Q = ∑ y - A = 60 × 20 × 50 = 60 × 10 3 m m ³

Com isso o fluxo de cisalhamento é:

q = V Q I t o t a l = 3000 × 60 × 10 3 11,84 × 10 6

q = 15,2 N / m m

A tensão de cisalhamento será então:

τ A = q t

Se liga só nisso aqui, t é a espessura por onde passa o fluxo de cisalhamento. A peça a esquerda é colada em três peças a direita com espessura de 20mm. Porém a gente tem que se ligar que a peça do meio não possui momento estático. Sendo assim a tensão vai se dividir na parte de cima e na parte de baixo e por isso:

t = 2 × 20 = 40 m m

τ A = 15,2 40 = 0 , 380 M P a = 380 k P a

Resposta

  1. τ A = 380 k P a
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolva o Problema 11.6 se a seção transversal tiver largura desconhecida, mas tiver de ser quadrada, isto é,h = b
A viga de madeira de ser carregada como mostra a figura. Se as extremidades suportarem somente forças verticais, determine o maior valor de P que pode ser aplicado. σ a d m = 25 M P a ,τ a d m = 700k
A viga de madeira tem seção transversal retangular e é usada para suportar uma carga de 6 kN. Se a tensão de flexão admissível for σ = 14M P a , τ = 5M P a , determine a altura h da seção transversal
A viga simplesmente apoiada é feita de madeira com tensão de flexão admissível σ a d m = 7M P a e a tensão de cisalhamento admissível τ a d m = 0,5M P a . Determine as dimensões da viga se ela tiver d
Selecione no Apêndice B a viga de aço de abas largas de menor peso que suportará com segurança as cargas mostradas na figura, na qual w = 100 k N m e P = 25k N . A tensão de flexão admissível é σ a d