Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas Revisão - Ex. 202

Uma única força P é aplicada à barra de aço mostrada. Três sensores elétricos localizados em A, B e D indicam as seguintes deformações específicas:

ε A = 800   μ                                                             ε B = 400   μ                                                                   ε C = 200   μ

Sabendo-se que E = 200 GPa, determinar a intensidadde de P e a sua linha de ação.

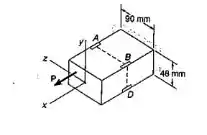
Passo 1

Falaaaa... belezinha???

Pra resolver essa questão vamos precisar do momento de Inércia (retângulo):

I = 1 12 b h 3

E também, pra tensão, temos:

σ = E ε

Ahh... e falta a equação com os momentos e tals...

σ x = P A - M z y I z + M y z I y

Então mão a obra...

Passo 2

Calculando os momentos de inércia:

I y = 1 12 0,048 0,090 3

→ I y = 2,92 × 10 - 6   m 4

I z = 1 12 0,090 0,048 3

→ I z = 0,83 × 10 - 6   m 4

Para a área:

A = 0,090 0,048

→ A = 4,32 × 10 - 3   m 2

Para os momentos, como P é de tração:

M y = P z

M z = - P y

(esse x e esse y não temos, mas depois vamos achar, que vai ser a tal linha de ação)

As posições dos sensores:

y A = 0,024   m ; z A = 0,045   m

y B = 0,024   m ; z B = - 0,045   m

y D = - 0,024   m ; z D = - 0,045   m

Passo 3

Achando as tensões:

σ A = 200 × 10 9 800 × 10 - 6

→ σ A = 16 × 10 7   P a

σ B = 200 × 10 9 400 × 10 - 6

→ σ C = 8 × 10 7   P a

σ D = 200 × 10 9 200 × 10 - 6

→ σ D = 4 × 10 7   P a

E na equação com os momentos:

σ A = P A - M z y A I z + M y z A I y

σ B = P A - M z y B I z + M y z B I y

σ D = P A - M z y D I z + M y z D I y

Passo 4

Se fizermos:

σ A - σ B = P A - M z y A I z + M y z A I y - P A - M z y B I z + M y z B I y

σ A - σ B = - M z y A I z + M y z A I y + M z y B I z - M y z B I y

σ A - σ B = M z I z y B - y A + M y I y z A - z B

16 × 10 7 - 8 × 10 7 = M z 0,83 × 10 - 6 0,024 - 0,024 + M y 2,92 × 10 - 6 0,045 + 0,045

16 × 10 7 - 8 × 10 7 = M y 2,92 × 10 - 6 0,045 + 0,045

→ M y = 2596   N ⋅ m

σ B - σ D = P A - M z y B I z + M y z B I y - P A - M z y D I z + M y z D I y

σ B - σ D = - M z y B I z + M y z B I y + M z y D I z - M y z D I y

σ B - σ D = M z I z y D - y B + M y I y z B - z D

8 × 10 7 - 4 × 10 7 = M z 0,83 × 10 - 6 - 0,024 - 0,024 + M y 2,92 × 10 - 6 - 0,045 + 0,045

8 × 10 7 - 4 × 10 7 = M z 0,83 × 10 - 6 - 0,024 - 0,024

→ M z = - 692   N ⋅ m

Jogando em uma das 3, pra achar o P :

σ A = P A - M z y A I z + M y z A I y

16 × 10 4 = P 4,32 × 10 - 3 - - 0,692 0,024 0,83 × 10 - 6 + 2,596 0,045 2,92 × 10 - 6

→ P = 432 × 10 3   N

→ P = 432   k N

Passo 5

Agora falta a linha de ação, né...

Mas temos que:

M y = P z

2596 = 432 × 10 3 z

→ z = 0,006   m

→ z = 6   m m

M z = - P y

- 692 = - 432 × 10 3 y

→ y = 0,0016   m

→ y = 1,6   m m

Ufaaa... Essa deu um trabalhão, heim... Mas dá uma respirada e vamos partir pra outra???

Resposta

P = 432   k N

z = 6   m m

y = 1,6   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sabendo-se que a carga de 120k N pode ser aplicada a qualquer ponto da circunferência de raio 40 m m mostrada, determinar:A correspondente tensão em A ,BeD
Para o carregamento mostrado, determinar:b) o ponto onde a linha neutra intercepta a linha ABD
Para o carregamento mostrado, determinar:A tensão nos pontos A e B;
Resolver o P r o b .4.156 , considerando que a intensidade a força aplicada em G é aumentada de1100N para 1780 N .A tensão nos pontos A e B;
Uma carga axial P é aplicada como mostrado a um cirto perfil estrutural, em forma de T . Determinar (b) o ponto correspondente onde a linha neutra intercepta a linha A B . (Dados: A = 4450m m 2 ; I y