Para o dado estado plano de deformação, usar o método da para determinar o estado de deformação associado aos eixos e , que foram girados de um ângulo , no sentido mostrado.
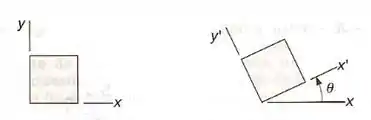
Passo 1
Fala galerinha, pode parecer que agora vamos ver algo muito complexo, mas na verdade continua sendo o que já sabemos, agora só vamos usar um novo conceito.
Pensa no seguinte, sempre que alguém pedia pra você fazer uma transformação de tensões, você já sabia de cabeça as fórmulas que tinha que usar, que são essas aqui de baixo:
Ou seja, o que essa fórmula representa? Ela me dá as tensões linha (,,) em função do estado plano de tensões iniciais ( ou seja, conseguimos relacionar o que tínhamos antes, com um novo estado quando fazemos a rotação.
Nesse exercício vamos fazer a mesma coisa, PORÉM, agora estamos olhando um estado plano de DEFORMAÇÕES, ou seja, o principio é exatamente o mesmo do estado de tensões, mas agora vamos ver as deformações, e nesse caso também temos fórmulas pra nos auxiliar, e elas são dadas por:
E por fim só precisamos lembrar o seguinte, se o ângulo gira no sentido anti-horário, usamos o ângulo positivo, e se girar no sentido horário, usamos o ângulo negativo.
Agora que já sabemos isso, vamos ao nosso problema.
Passo 2
Sendo assim, sabemos que os dados do enunciado são dados por:
Substituindo nas nossas equações teremos que:
E assim determinamos o estado de deformações da nossa estrutura quando giramos ela de 60° no sentido horário, beleza? Bora pro próximo exercício?