Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 2.Problemas - Ex. 3
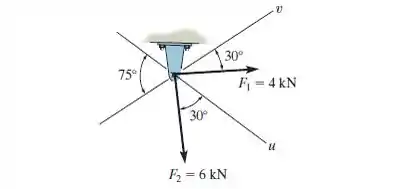
Decomponha em componentes ao longo dos eixos e , e determine suas intensidades.
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a primeira questão de mais um livro juntos!
Nessa questão nós precisamos calcular as componentes da força na direção e .
A vida é tão mais fácil quando o sistema de coordenadas é ortogonal (ângulos de 90°) ...
Mas, não fiquem abatidos! Vamos resolver facilmente também!
A chave desta questão é trabalhar com a geometria do problema. Temos que desenhar no nosso esboço o triângulo de lados dados pelo vetor e seus componentes nos eixos e . A partir das informações obtidas conseguiremos calcular tudo pela lei dos senos.
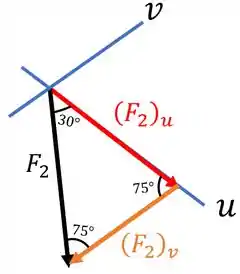
Então, muito cuidado na hora do esboço!!! Vejamos só ele abaixo:
Passo 2
Agora que já obtemos o nosso triângulo, basta aplicarmos a lei dos senos para calcular cada um dos vetores decompostos.
Pela lei dos senos nós temos:
E então,
Substituindo os valores, obtemos:
E assim finalizamos a questão!