Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 2.Problemas - Ex. 5
Se a intensidade da força resultante deve ser 500 N direcionada ao longo do eixo positivo, determine a intensidade da força e sua direção .
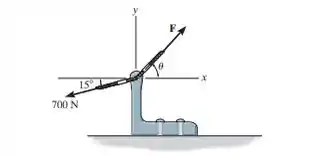
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a primeira questão de mais um livro juntos!
Nessa questão nós precisamos determinar quem é a força e qual sua intensidade. Para isto, sabemos que a força resultante deve ter intensidade de 500 N e direcionada ao longo do eixo positivo.
Em outras palavras, a componente da resultante na direção é nula!
A forma mais fácil de resolvermos ambas as perguntas simultaneamente é escrevermos as forças em termos das componentes em e . Para isto, vamos usar e abusar da trigonometria e da geometria do problema!
Depois, podemos somar componente com componente (e simultaneamente para as componentes ), e igualar ao que sabemos da força resultante. Assim, teremos um sisteminha simples, e a sua resposta é o que buscamos!
Então, vamos as contas!!!
Passo 2
Vamos agora decompor as forças e em relação as suas componentes e . Portanto,
Tomem muito cuidado aqui com relação aos ângulos utilizados e os sinais das componentes para que não errem ao decompor!
Passo 3
Agora que decompomos as duas forças já podemos realizar a soma delas.
Só que temos uma grande vantagem. Como dissemos lá no Passo 1, só podemos somar componente com componente (e o mesmo é válido para ). Portanto,
Lembrando que a força resultante possui componente apenas em positivo, isto é, e , temos:
Resolvendo a segunda equação obtemos . E assim, temos que a intensidade da força é:
E assim finalizamos a nossa questão!