Enunciado

Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 2.Problemas - Ex. 25

Se a força resultante dos dois rebocadores é 3 kN, direcionada ao longo do eixo x positivo, determine a intensidade da força exigida e sua direção .

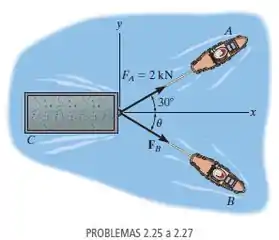
Fonte: Estática Mecânica para Engenharia – 14ª ed

Passo 1

E aí galerix, vamos que vamos!!

Bora lá!

Bem, a respeito de decomposição de forças, mais uma vez vamos lembrar, até abusar, sempre das 3 coisas para a melhor resolução de problemas envolvendo força resultante (é repetitivo, mas muito importante kkk):

Regra do paralelogramo;
Lei dos senos;
Lei dos cossenos.

E lembrando que, nesse capítulo, serão de suma importância a aplicação dessas 3 leis e regras.

O problema quer a intensidade da força , já sabendo que a resultante .

Passo 2

Devemos atentar ao detalhe: A resultante é direcionada ao longo do eixo x positivo.

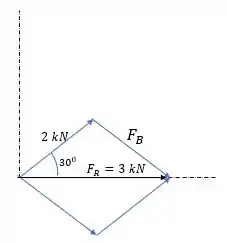
Usando a Lei dos Cossenos, podemos encontrar o valor de :

Assim, temos:

Resposta

Portanto:

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Derive as expressões a seguir utilizando álgebra vetorial: cos ⁡ α - β = cos ⁡ α cos ⁡ β + s e nαs e nβ s e n α - β = s e nα cos ⁡ β - cos ⁡ α s e nβ

Encontre os componentes do vetor de aceleração a em coordenadas esféricas.

Demonstre que ∫ 2 a r ∙ r ˙ + 2 b r ˙ ∙ r ¨ d t = a r 2 + b r ˙ 2 + c o n s t a n t e onde r é o vetor da origem ao ponto (x1, x2, x3). As quantidades r e r ˙ são as magnitudes dos vetores r e r ˙ , r

Considere as matrizes a seguir:A = ([[1,2,-,1],[0,3,1],[2,0,1]]) , B = ([[2,1,0],[0,-,1,2],[1,1,3]]) , C = ([[2,1],[4,3],[1,0]]) Determine:a ) |A B| b ) A C c ) A B C d ) A B - B^t A^t

Uma partícula se move com v = constante ao longo da curva r = k(1 + cos θ) (uma cardioide). Encontre: r ¨ ∙ e r = a ∙ e r ,aeθ ˙