Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 7.Problemas - Ex. 19
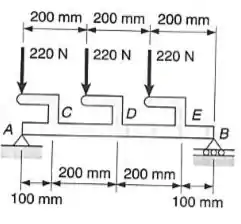
Desenhar os diagramas de força cortante e do momento fletor para a viga AB, submetida ao carregamento indicado.
Passo 1
E ai gurizada tudo beleza? Espero que sim!!
Bom olha só, como no diagrama do exercício temos força aplicada na barra. Portanto vamos encontrar as reações em A e em B (VA e VB)... Considerando a setinha para baixo com valores negativos ..
Primeiramente VB, pode ser? Seguindo a mesma lógica (carga x comprimento).
Agora somatório de forças em Y (vertical) para encontrarmos VA (nesse caso somando só as forças).
Passo 2
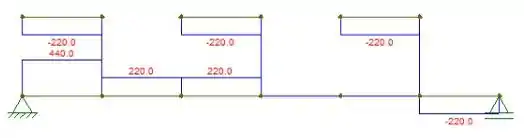
Agora vamos determinar a força cortante? Vem comigo!!!
Para realizarmos esse diagrama pensem comigo, eu falei para vocês antes que a seta para baixo é negativo certo?
Então no 1º quadrante fica igual= a VA pois temos um apoio antes da carga=
2º quadrante: como temos a reação VA positiva, o cálculo da força será assim:
3º quadrante: usamos o resultado anterior menos a força aplicada:
4º quadrante: a própria reação VB=
Primeiramente é necessário fazer a análise apenas nas barras superiores e dessa forma encontrar o esforço cortante, para encontrar o esforço cortante na barra inferior deve-se estar atento que a carga nas barras superiores se transferem para essas barras causando o esforço cortante. Isso se justifica a descontinuidade no diagrama abaixo das barras inferiores...
Passo 3
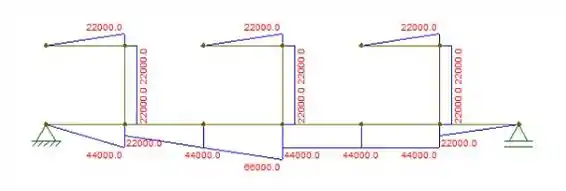
Agora vamos calcular comigo o momento fletor, 3 reações= 3 momentos, basta multiplicarmos a força pela distância expressa no diagrama, para todos os pontos.
MA=0 não tem nenhuma distância, a carga é aplicada em um ponto de “Y=0”
Agora calculando em “C” (da esquerda para a direita)
Agora calculando em “D”
Agora calculando em “E”
Agora sim podemos desenhar o diagrama
Resposta
Ei, a resposta está no passo a passo :)