Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 7.Problemas - Ex. 146
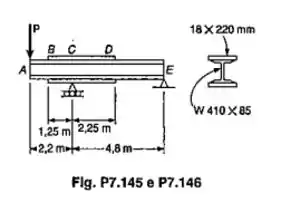
Duas placas de cobertura, cada uma com de espessura e de largura, soldadas a uma viga de perfil laminado como mostrado. Sabendo-se que e , determinar a maior força vertical , que pode ser aplicada no ponto da viga mostrada.
Passo 1
Fala aí galera, bora pra mais uma questão de Resmat.
Para resolvermos este problema, precisamos encontrar a máxima força . Para isso, temos que encontrar o módulo resistente da seção , dado por:
Entretanto, como temos uma figura composta pelo perfil e mais duas placas de cobertura. Podemos encontrar por tabela que:
Com esse valor, podemos encontrar seu momento de inércia:
Então, aplicamos o teorema dos eixos paralelos a fim de obtermos o momento de inercia das vigas com as coberturas. Temos:
Onde é a área de cada barra e é a distância entre o centro da viga até o centro da barra:
Logo:
Agora, podemos encontrar o módulo de resistência. Fica assim:
Passo 2
Em seguida, vamos calcular o momento fletor máximo que esta viga suporta. Pelo DCL, temos:
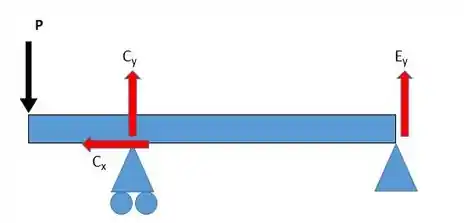
Podemos perceber que a força é nula pois esta é a única força em . Agora, vamos partir para o somatório das forças em :
Para o momento, temos:
Passo 3
Agora, vamos calcular a máxima tensão normal, dada por:
Vamos calculá-lo em , temos:
E assim, substituímos para encontrarmos , temos: