Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 15.2 - Ex. 32

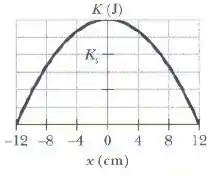
A figura mostra a energia cinética K de um oscilador harmônico simples em função da posição x . A escala vertical é definida por K s = 4,0   J . Qual é a constante elástica?

Passo 1

Fala galerildis, tudo jóinha?

Nessa questão aqui, o segredo é a gente lembrar o seguinte: a energia total do sistema é conservada. Ou seja:

E = K + U

Onde os valores de K (energia cinética) e U (energia potencial) mudam, mas a soma deles é sempre a mesma.

Passo 2

Belezoca, nós também sabemos o seguinte: quando a energia cinética é máxima, a energia potencial é zero!

(Pode ser, por exemplo, o momento em que um pêndulo passa pelo ponto mais baixo da trajetória: a velocidade é máxima, e a energia potencial é zero).

Então beleza:

E = K m á x + 0

Olhando o gráfico (em que cada traço no eixo vertical “vale” 1,0   J ), qual é a energia cinética máxima?

K m á x = 6,0   J

Ou seja:

E = 6,0   J

Passo 3

Ok, agora já sabemos qual é a energia total do sistema. Só precisamos lembrar da fórmula que relaciona esse valor com a constante k :

E = 1 2 k x m 2

k = 2 E x m 2

Agora fica faltando só achar o valor da amplitude. Mas não tem estresse, no gráfico dá pra ver que a amplitude do movimento é:

x m = 12   cm

x m = 0,12   m

Então:

k = 2 6,0 0,12 2

k = 8,3 × 10 2   N/m

Prontinho!

Resposta

k = 8,3 × 10 2   N/m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um oscilador harmônico simples é formado por um bloco preso a uma mola com k = 200N / m . O bloco desliza em uma superfície sem atrito, com o ponto de equilíbrio em x = 0 e uma amplitude de 0,20m . O
Se o ângulo de fase de um sistema massa-mola em MHS é π / 6 r a d e a posição do bloco é dada por x = x m c o s ω t + ϕ , qual é a razão entre a energia cinética e a energia potencial no instante t=0?
Uma mola de massa desprezível está pendurada no teto com um pequeno objeto preso à extremidade inferior. O objeto é inicialmente mantido em repouso em uma posição y , tal que a mola se encontra no est
A Fig. 15-51 mostra a posição de um bloco de 20 g oscilando em um MHS na extremidade de uma mola. A escala do eixo horizontal é definida por t s = 40,0 m s . Qual é (a) a energia cinética máxima do bl
Um bloco está em MHS na extremidade de uma mola, com a posição dada por x = x m c o s ω t + ϕ . Se ϕ = π / 5 r a d , que porcentagem da energia mecânica total é energia potencial no instante t = 0 ?