Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.8 - Ex. 194

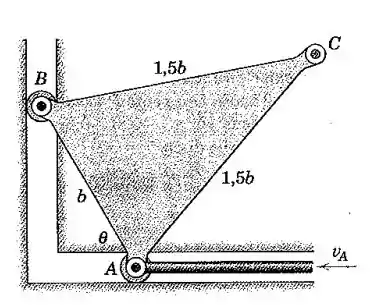
A placa em formato de triângulo isósceles é guiada pelos dois roletes nos vértices A e B que estão limitados a se deslocar nas ranhuras perpendiculares. A barra de controle fornece a A uma velocidade constante v A para a esquerda durante um intervalo do movimento. Determine o valor de θ para o qual a componente horizontal da velocidade de C é zero.

Passo 1

Bom pessoal, esta questão é bastante geométrica. Então, vamos fazer um esboço do sistema:

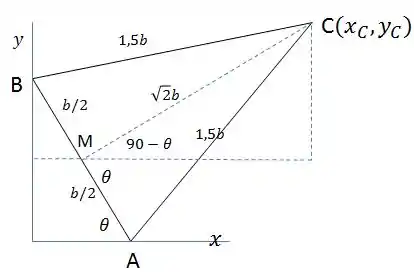
Bom, traçamos a mediana CM e calculamos seu módulo por:

C M = 1,5 b 2 - b 2 2 = 2 b

As coordenadas do ponto C são muito importante nesta questão, pois podemos calcular a velocidade do ponto a partir de suas derivadas em função do tempo.

Pela figura, temos que as coordenadas do ponto C são:

x C = b 2 c o s θ + 2 b c o s 90 - θ = b 2 c o s θ + 2 b s e n θ

y C = b 2 s e n θ + 2 b s e n 90 - θ = b 2 s e n θ + 2 b c o s ( θ )

Entretanto, a questão pede para encontrar θ quando a componente velocidade na horizontal vale zero. Portanto, apenas a componente em x nos interessa. Podemos encontrar a velocidade na horizontal através da derivada de x C :

x C ˙ = - b 2 s e n θ + 2 b c o s ( θ )

Para a velocidade ser nula:

x C ˙ = 0 = - b 2 s e n θ + 2 b c o s ( θ )

b 2 s e n θ = 2 b c o s ( θ )

tan ⁡ θ = 2 2

θ = 70,5 °

Resposta

θ = 70,5 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

15.53. O braço ACB gira em torno do ponto C com velocidade angular de 40 rad /s no sentido anti-horário. Dois discos de atrito A e B estão presos por pinos em seus centros ao braço ACB do modo mostrad
15.55. Sabendo que a manivela AB tem uma velocidade angular constante de 160 rpm no sentido anti-horário, determine a velocidade angular da barra BD e a velocidade do colar D quando (a) 0, (b) 90°.
15.57. No sistema biela-manivela de motor mostrado na figura, l 160 mm e b 60 mm. Sabendo que a manivela AB gira com uma velocidade angular constante de 1.000 rpm no sentido horário, determine a veloc
15.56. Sabendo que a manivela AB tem uma velocidade angular constante de 160 rpm no sentido anti-horário, determine a velocidade angular da barra BD e a velocidade do colar D quando (a) 60°.
15.61. Uma cremalheira reta repousa sobre uma engrenagem de raio r 60 mm e está presa ao bloco B como mostra a figura. Sabendo que nesse instante a velocidade do bloco B é de 200 mm/s para a direita e