Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.6 - Ex. 40
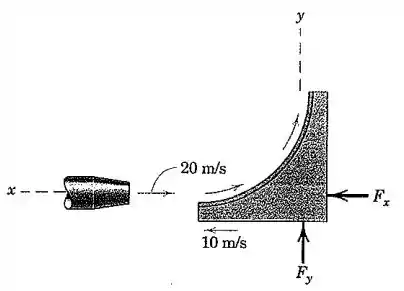
A pá com se desloca para a esquerda com uma velocidade constante de contra uma corrente de água doce escoando com uma velocidade de a partir do bocal com de diâmetro. Calcule as forças e sobre a pá exigida para suportar o movimento.
Passo 1
Lembre-se de que a taxa de escoamento de massa deve considerar a velocidade relativa da corrente em relação à pá, não a velocidade absoluta da corrente, então:
Passo 2
Agora, se analisarmos apenas a direção , a corrente entra com velocidade e sai somente com a velocidade , devida ao movimento da pá, então:
E em , a corrente entra sem nenhuma velocidade nesse direção, mas sai com a mesma velocidade relativa , conforme calculado no passo anterior, então:
Resposta
Exercícios de Livros Relacionados
Se a massa de um homem é 90k g , determine o seu peso em newtons e calcule a sua massa correspondente em s l u g s .
Calcule a aceleração devida à gravidade em relação à Terra girando e o valor absoluto se a Terra não estivesse girando, para uma posição ao nível do mar em uma latitude norte ou sul de 45 ° .
A massa de uma dúzia de maçãs é 2k g . Determine o peso médio de uma maçã em ambas as unidades SI e do sistema americano. No presente caso, quão aplicável é a “regra prática” de que uma maçã média pes
Considere duas esferas de ferro, cada uma com diâmetro de 100m m , que estão apenas se tocando. A que distância r do centro da Terra a força de atração mútua entre as esferas em contato será igual à f
Um alpinista tem uma massa de 80k g . Determine sua perda de peso absoluto ao ir desde o pé do Monte Everest a uma altitude de 2440 metros até o seu topo a uma altitude de 8848m . O Monte Everest tem