Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.6 - Ex. 44

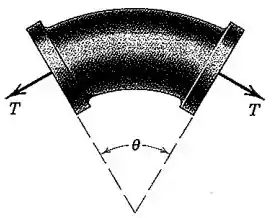
O tubo curvo mostrado possui uma área de seção transversal A e está suportado em seu plano pela tração T aplicada a seus flanges pelos tubos adjacentes aos quais está conectado (não mostrados). Se a velocidade do líquido é v , sua massa específica ρ , e sua pressão estática p , determine T e mostre que é independente do ângulo θ .

Passo 1

No tubo, atuam as forças de tração T e hidrostática p A , conforme mostra a figura a seguir:

Porém, repare que o líquido sai com a mesma velocidade horizontal que entra no tubo. A alteração de velocidade se dá apenas na direção vertical, de modo que só analisaremos as forças e a variação de quantidade de movimento nessa direção vertical y .

Então, de acordo com a geometria da figura, teremos:

∑ F y = 2 T   s e n θ 2 - 2 p A   s e n θ 2

∑ F y = 2 T - p A   s e n θ 2

Beleza?

Passo 2

Agora, lembre-se de que a variação na quantidade de movimento vertical do sistema será:

G ˙ y = m ' Δ v y

Mas a taxa de escoamento m ' é:

m ' = ρ A v

E a variação de velocidade em y será:

Δ v y = v   s e n θ 2 - - v   s e n θ 2

Δ v y = 2 v   s e n θ 2

Logo,

G ˙ y = m ' Δ v y = ρ A v 2 v   s e n θ 2

G ˙ y = 2 ρ A v 2 s e n θ 2

Passo 3

Então, vamos lembrar que:

∑ F y = G ˙ y

2 T - p A   s e n θ 2 = 2 ρ A v 2 s e n θ 2

T - p A = ρ A v 2

T = A   p + ρ v 2

Resposta

T = A   p + ρ v 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Descreva como determinar se um equilíbrio é estável ou instável de acordo com d2U/dx2.
Duas estrelas ligadas gravitacionalmente com massas diferentes m1 e m2, separadas por uma distância d, giram ao redor do seu centro de massa em órbitas circulares. Demonstre que o período τ é proporci
A velocidade de uma partícula de massa m varia com a distância x conforme v(x) = ax-n. Suponha v(x = 0) = 0 em t = 0.Determine a força F(x) responsável.Determine x(t).E F(t).
Resolva o Exemplo 2.12 utilizando forças em vez de energia. Como é possível determinar se o equilíbrio do sistema é estável ou instável?
Um barco com velocidade inicial é empurrado em um lago. Ele tem a sua velocidade reduzida pela água por uma força F = - α e β v .Determine uma expressão para a velocidade v(t).Determine o tempo para o