Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.6 - Ex. 39

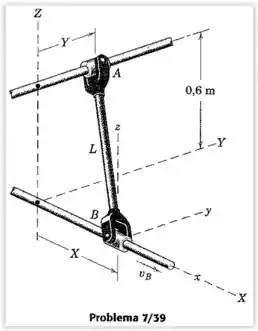
Para o instante representado, o cursor B está se deslocando ao longo da haste fixa na direção X com uma velocidade constante v B = 4   m / s . Também neste instante X = 0,3   m e Y = 0,2   m . Calcule a velocidade do cursor A , que se desloca ao longo da haste fixa paralela ao eixo Y . Resolva primeiro por meio da diferenciação da relação X 2 + Y 2 + Z 2 = L 2 com relação ao tempo e depois usando a primeira das Eqs. 7/4 com eixos em translação fixados a B . Cada garfo é livre para girar em relação ao eixo da barra.

Passo 1

Apenas tentando observar o problema, temos que quando o cursor B se desloca na direção X , teremos o cursor A se deslocando na direção – Y , visando manter L constante.

Outra coisa que devemos lembrar das nossas aulas de cálculo é a regra da cadeia, ou seja

d X n d t = n ⋅ X n - 1 ⋅ X ˙

Onde

X ˙   ≡ d X d t

Passo 2

Vamos inicialmente diferenciar a relação X 2 + Y 2 + Z 2 = L 2 em termos de t .

2 X X ˙ + 2 Y Y ˙ + 0 = 0

Como as barras são fixas em Z e seu comprimento L é constante, suas derivadas temporais são nulas.

Assim ficamos com

Y ˙ = - X Y X ˙ → v A = - X Y v B

Logo no instante dado em X = 0,3 m e Y = 0,2   m com v B = 4   m / s

Temos que

v A = - 6   m / s

Exatamente como tínhamos suposto no Passo 1.

Passo 3

A primeira Eq. 7/4 temos que

v A → = v B → + ω → × r → A / B

Se o giro da haste não ocorrer em seu eixo de simetria, o que é o nosso caso, ω sempre será perpendicular ao eixo principal da barra que é definido pelo comprimento L . Isso implica que

ω → ⋅ r → A / B = 0

Ou seja,

ω x   ( - 0,3 ) + ω y   0,2 + ω z   0,6 = 0

Devemos calcular o determinante da matriz a baixo. Para isso vamos usar o método dos cofatores.

ω × r → A / B = d e t i ^ j ^ k ^ ω x ω y ω z - 0,3 0,2 0,6

i ^ ω y ⋅ 0,6 - ω z ⋅ 0,2 -   j ^ ω x ⋅ 0,6 - ω z ⋅ - 0,3 +   k ^ ( ω x ⋅ 0,2 - ω y ⋅ ( - 0,3 ) ) ^ = 0

Como sabemos que v A → = j   ^ v A e v B → =   i ^   v B

Temos que

ω y ⋅ 0,6 - ω z ⋅ 0,2 = -   v B

Pois queremos anular o termo v B → da Equação 7/4

  ω x ⋅ 0,6 - ω z ⋅ ( - 0,3 ) = v A

Pois é o que sobra ao lado esquerdo da nossa equação v A → = v B → + ω → × r → A / B se encontra apenas na direção Y

ω x ⋅ 0,2 - ω y ⋅ ( - 0,3 ) = 0

Pois não há velocidade na direção Z .

Isolando ω z e ω x da segunda e quarta equação encontrada respectivamente e substituindo na primeira, ficamos com

ω y ( - 0,3 ) 0,2   ( - 0,3 ) +   ω y   0,2 +   ω y 0,6 0,2   0,6 + v B 0,2 = 0

Implicando que ω y =   - 8,16   r a d / s

Logo temos pela quarta relação que ω x = - 12,24   r a d / s e pela segunda relação ω z = 4,48   r a d / s

Logo pela terceira equação temos que

- 8,16 0,6 - 4,48 0,3 =   - 4,896 - 1,344 =   - 6

Logo temos que v A =   - j   ^ 6 m / s

Resposta

v A =   -   j ^   6   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A placa quadrada de 20 kg está presa por um pino ao anel liso de 5 kg. Determine a aceleração inicial da placa quando P = 100N for aplicada ao anel. A placa está originalmente em repouso.
A placa quadrada de 20 kg está presa por um pino ao anel liso de 5 kg. Determine a aceleração angular inicial da placa quando P = 100 n for aplicada ao anel. A placa está originalmente em repouso.
A bobina tem uma massa de 100 kg e um raio de giração K g=200m m em relação a seu centro de massa G. Se uma força vertical P=200N for aplicada ao cabo, determine a aceleração de G e a aceleração angul
A bobina tem uma massa de 100 kg e um raio de giração K g=200m m em relação a seu centro de massa G. Se uma força vertical P=500N for aplicada ao cabo, determine a aceleração de G e a aceleração angul
O cilindro maciço possui um cone do corpo com um semi-ângulo do vértice de 20º. Em um determinado instante a velocidade angular ω tem um módulo de 30 rad/s e está situada no plano y - z . Determine a