Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 8.Problemas - Ex. 66

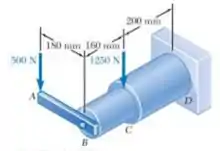
Desprezando o efeito dos adoçamentos e das concentrações de tensões, determine os menores diâmetros permissíveis para as hastes sólidas BC e CD. Utilize T a d m = 60 M P a .

Passo 1

E ai gurizada tudo bem? O enunciado pede que a gente determine menores diâmetros permissíveis para as hastes sólidas BC e CD. Vamos ao nosso querido esboço :D

τ a l l = 60 × 10 6 P a

J c = π 2 c 3 = M 2 + T 2 τ a l l

c 3 = 2 π M 2 + T 2 τ a l l                     d = 2 c

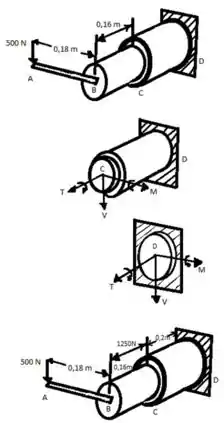
Passo 2

Esquerda do C: M = 500 0,16 = 80 N ∙ m

T = 500 0,18 = 90 N ∙ m

M 2 + T 2 = 120,416 N ∙ m

Esquerda de D: T = 90 N ∙ m

M = 500 0,36 + 1250 0,2 = 430 N ∙ m

M 2 + T 2 = 439,32 N ∙ m

Passo 3

Menor diÂmetro d B C .

c 3 = 2 120,416 π 60 x 10 6 = 1,27765 x 10 - 6 m 3

c = 0,01085 m = 10,85 m m

d B C = 21,7 m m

Menor diÂmetro d C D .

c 3 = 2 439,32 π 60 × 10 6 = 4,6613 × 10 - 6 m 3

c = 0,01670 m = 16,7 m m   d C D = 33,4 m m

Resposta

d B C = 21,7 m m

d C D = 33,4 m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolva o problema 8.78 se a seção transversal for quadrada de dimensões 6mm por 6mm
A viga de abas largas está sujeita à carga mostrada na figura. Determine as componentes da tensão nos pontos A e B e mostre os resultados em um elemento de volume em cada um desses pontos. Use a fórmu
O pino de suporte sustenta a carga de 3,5 kN. Determine as componentes da tensão no elemento estrutural do suporte no ponto A. O suporte tem 12 mm de espessura.
O bloco está sujeito às duas cargas axiais mostradas na figura. Faça um rascunho da distribuição da tensão normal que age na seção transversal no corte a-a. Despreze o peso do bloco.
O pino de suporte sustenta a carga de 3,5 kN. Determine as componentes da tensão no elemento estrutural do suporte no ponto B. O suporte tem 12 mm de espessura.