Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 8.Problemas - Ex. 31
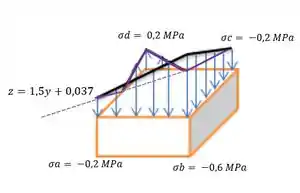
O bloco está sujeito às duas cargas axiais mostradas na figura. Faça um rascunho da distribuição da tensão normal que age na seção transversal no corte a-a. Despreze o peso do bloco.
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora.
Bom, nosso enunciado nos diz que esse bloquinho é cortado pelo plano a-a e recebe duas forças aplicadas nos pontos B e D, e nos pede os desenhos para ver a distribuição da tensão normal nessa seção.
O que acontece ali é que temos duas forças normais a nossa seção e talvez elas gerem momentos. Essas duas coisinhas geram tensão normal.
A parada é a gente descobrir esses esforços na seção e achar as tensões normais causadas por eles.
Vamos!!
Passo 2
Nosso primeiro passo vai ser achar nossas cargas internas N, My e Mz. Vamos considerar que é o eixo da nossa seção paralela ao lado de .
Passo 3
Agora que já temos nossas cargas internas definidas, vamos calcular as tensões resultantes em cada uma das quinas do bloquinho. Com a tensão nesses pontos, a gente consegue fazer nosso esboço.
causa compressão. Então ele entra negativa. Precisamos só identificar o sinal da tensão normal causada pelo momento em cada um desses pontos. Vamos fazer um esquema
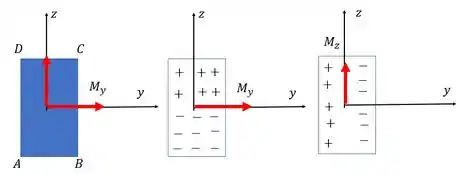
Esses sinais de menos dizem que a gente tem compressão na região. E o de mais temos tração.
Para achar onde é tração ou compressão, você coloca seu dedão da mão direita na direção do vetor momento. Ao girar a mão, a região de compressão é onde seus dedos entram no plano da folha.
No , temos que a tensão causada por é positiva e é negativa. Substituindo os dados na fórmulinha, ficamos assim:
No , temos que a tensão causada por e é negativa. Substituindo os dados na fórmulinha, ficamos assim:
Fazendo um pesamento análogo para os outros pontos:
Passo 4
Com esses pontos, a gente pode desenhar nossa distribuição de tensão. Uma coisa que é importante nesse desenho é achar a linha neutra, onde a tensão normal zera.
Uma forma de fazer isso é pegar a fórmula do nosso ponto que está no primeiro quadrante dos eixos e igualar a zero. Esse ponto é o :
A gente vai substituir nossos dados aí, exceto as coordenadas, que vamos deixar como e . E igualar a tensão a zero
Isolando , ficamos aproximadamente com a equação:
Com ela e nossos pontos, o esboço fica assim:
A setinha para baixo indicam que há compressão. E a gente ligou os pontos por retas, porque a distribuição de tensão nesse caso é linear 😉
Resposta
