Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 11.Problemas - Ex. 39
Determinar o ângulo para haver equilíbrio e investigar a estabilidade nessa posição. As hastes possuem massa de cada e a mola tem comprimento não deformado de .
Passo 1
Fala galera, tudo certo? Bora fazer mais um exercício? Prometo que vai ser bem rapidinho!
O enunciado nos pede para determinar o ângulo necessário para que o corpo esteja em equilíbrio e, posteriormente, avaliar a estabilidade para essa posição. Considerando que a mola não deformada tem comprimento igual a e as hastes possuem massa de .
Então bora lá! Para resolver esse problema, vamos começar analisando o diagrama de corpo livre:
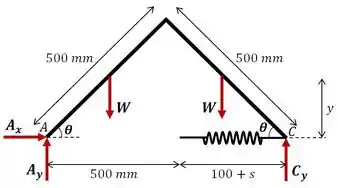
Onde a distância é:
A deformação da mola, por sua vez, é dada por:
E o peso da haste:
Passo 2
Show de bola! Vamos começar então formulando a equação da energia potencial desse sistema. Como temos atuando apenas o peso da haste e a força exercida pela mola, a energia potencial do sistema é dada por:
Passo 3
Beleza, agora que nós temos a equação da energia potencial do sistema, para analisar o equilíbrio do corpo, podemos simplesmente fazer a derivada de em relação a e o resultado deve ser zero. Ou seja:
Resolvendo essa expressão encontramos:
Passo 4
Até aqui tudo certo né? Definimos o ângulo para que o sistema esteja em equilíbrio, para determinar a estabilidade do corpo, por sua vez, precisamos analisar derivada de segunda ordem da equação da energia potencial em relação a .
Neste caso existem três possibilidades:
Para a posição de equilíbrio com :
Logo, a estrutura está em equilíbrio, mas não está estável.
Já para a posição de equilíbrio com :
Logo, a estrutura está em equilíbrio e está estável.
É isso, galera. Até que foi de boa né?
Partiu pra próxima!
