Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 10.Problemas - Ex. 89

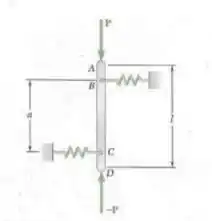
A barra vertical AD é fixada por duas molas de constante k e está em equilíbrio na posição mostrada. Determine o intervalo de valores da intensidade P para duas forças verticais iguais e opostas Pe — P para as quais a posição de equilíbrio é estável se (a) AB -CD. (b) AB= 2CD .

Passo 1

Fala aí galera, vamos para mais um problema de estática. Primeiro, temos o par de momentos:

M p = P l sin ⁡ θ

M F = - F a cos ⁡ θ

Portanto, temos:

d U = M p d θ + M F d θ

d U = P l sin ⁡ θ - F a cos ⁡ θ d θ

Temos que:

F = k s = k 1 2 a sin ⁡ θ

Substituindo:

d U = P l sin ⁡ θ - k 1 2 a sin ⁡ θ a cos ⁡ θ d θ

Passo 2

Para acharmos d V :

d V = - d U = - P l sin ⁡ θ d θ + 1 4 k a 2 sin ⁡ 2 θ d θ d V d θ = - P l sin ⁡ θ + 1 4 k a 2 sin ⁡ 2 θ d 2 V d θ 2 = - P l cos ⁡ θ + 1 2 k a 2 cos ⁡ 2 θ

Portanto, para θ = 0 :

d 2 V d θ 2 = - P l + 1 2 k a 2

Por fim, o equilíbrio é estávem em:

d 2 V d θ 2 > 0 ,         - P l + 1 2 k a 2 > 0

Resposta

- P l + 1 2 k a 2 > 0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Cada elemento tem uma massa por comprimento m 0 . Determine os ângulos θ e ϕ nos quais eles estão suspensos em equilíbrio. O contato em A é liso, e ambos são conectados por um pino em B .
Determine o ângulo θ para haver equilíbrio e investigue a estabilidade nessa posição. As hastes possuem massa de 3k g cada uma e o bloco suspenso D tem massa de 7k g . A corda D C tem comprimento tota
A haste uniforme tem massa de 100k g . Se a mola não estiver deformada quando θ = 60 ° , determine o ângulo θ para haver equilíbrio e investigue a estabilidade na posição de equilíbrio. A mola sempre
O bloco triangular de peso W se apoia sobre os cantos lisos que estão separados por uma distância a . Se o bloco possui três lados iguais de comprimento d , determine o ângulo θ para que haja equilíbr
As duas hastes possuem massa de 8k g cada. Determine a rigidez k exigida para a mola, de modo que haja equilíbrio quando θ = 60 ° . A mola tem comprimento de 1m quando não deformada. Investigue a esta