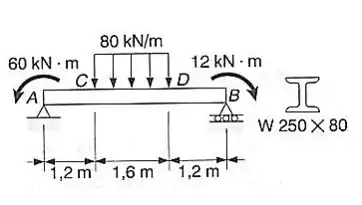
Para a viga com o carregamento mostrado, determinar: a) máximo tensão normal devido a flexão b) maior tensão de cisalhamento numa seção transversal devido à flexão.
Passo 1
E ai gurizada tudo beleza? Espero que sim!!
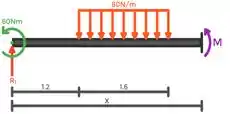
Para encontrarmos as reações nos apoios, é necessário verificar o equilíbrio de forças na vertical, para garantir que a viga não vai se mover nem para cima nem para baixo, e o equilíbrio de momentos, para garantir que a viga não irá girar. O diagrama de corpo livre da viga é:
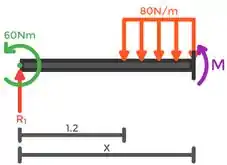
Partiu encontrar as reações, mas antes temos que transformar a carga distributiva em pontual, venha cmg!!!
Partiu encontrar as reações :D
Fazendo o equilíbrio dos momentos no primeiro apoio, encontra-se:
Galera um detalhe importante R1+R2= ou seja a soma das cargas aplicadas na viga ;)
Em que x¯x¯ representa a posição de aplicação equivalente da carga distribuída, que é o centroide da viga, então vamos calcular assim:
Substituindo os valores temos:
Das duas equações, encontra-se o seguinte sistema:
Resolvendo os sistemas achamos nossas reações R1 e R2 ;)
R1=76 KN
R2=52 KN
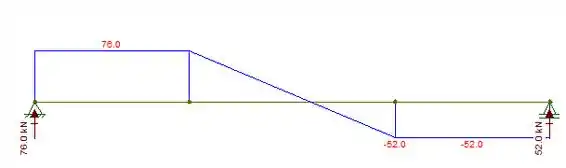
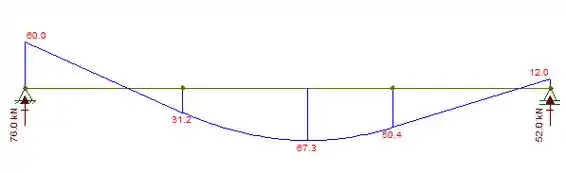
Agora sim galera, podemos encontrar o esforço cortante, vem comigo :D
Para realizarmos esse diagrama pensem comigo, eu falei para vocês antes que a seta para baixo é negativo certo? Lembrando da esquerda para a direita
Então no 1º quadrante fica temos: R1= 76 KN
2º quadrante:
3º quadrante:
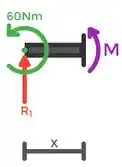
Agora vamos calcular comigo o momento, basta multiplicarmos a força pela distância expressa no diagrama, para todos os pontos.3reações = 3 momentos ;)
Passo 2
- Máximo tensão normal
- Maior tensão de cisalhamento
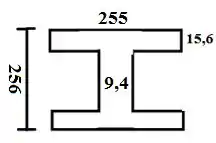
Galera lembrando que para vc encontrar a inércia deste perfil basta verificar o apêndice C do livro ;)
Passo 3
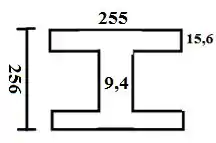
Onde Q encontramos da seguinte maneira: