Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 6.Problemas - Ex. 47

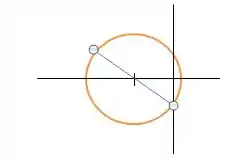
Determinar os planos principais e as tensões principais para o estado plano de tensões, resultante da superposição dos dois estados planos de tensões mostrado.

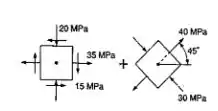
Passo 1

Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para analisarmos a figura e dizermos qual deveria ser a tensão pelo círculo de Mohr. Parece muita coisa, mas é tranquilo. Partiu??

Passo 2

Ok, nosso primeiro passo vai ser trazer os nossos valores pra cá pra analisar.

Pelo 1º estado, temos que:

σ x = 35   M P a

σ y = - 20   M P a

τ x y = - 15   M P a

Pelo 2º estado, temos que:

σ x = 20 + 20 cos ⁡ 45 ° - 15 + 15 sin ⁡ 45 ° = 8,54   M P a

σ y = 20 - 20 cos ⁡ 45 ° - 15 - 15 s in ⁡ 45 ° =   1,46   M P a

τ x y = 20 sin ⁡ 45 ° - 15 sin ⁡ 45 ° = 3,54   M P a

Agora falta calcularmos as tensões. Bora lá??

σ x = 43,54   M P a

σ y = - 18,54   M P a

τ z x = - 11,46   M P a

Passo 3

Pronto!! Agora é só fazermos umas matemágicas aí pra achar o resultado!!

Para desenhar o círculo de Mohr, vamos precisar das coordenadas.

σ w = 12,5   M P a

R = 16,96   M P a

tan ⁡ α = - 0,37     ∴       α = 2 0 , 3 °

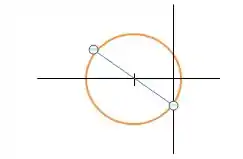
Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Desprezando-se o efeito da concentração de tensões no escalonamento, determinar os menores diâmetros permissíveis para as barras maciças B C e C D . Usar τ a d m = 60M P a .
Sabendo-se que o diâmetro do tronco de cone mostrado é 38m m em A e 58m m em B , determinar a máxima tensão de cisalhamento: ( a ) em A ; ( b ) em B .
Sabendo-se que as barras B C e C D têm diâmetros de 24m m e 36m m , respectivamente, determinar a máxima tensão de cisalhamento em cada uma barra. Desprezar o efeito da concentração de tensões no esca
Sabendo-se que τ a d m = 50M P a , determinar o menor diâmetro permissível para o eixo maciço A B , quando P = 670N , l = 460m m e L = 75m m . Incluir o efeito das tensões de cisalhamento, causadas pe
Usando τ a d m = 50M P a , dimensionar um tronco de cone para o carregamento mostrado, determinando o diâmetro necessário: ( a ) em A ; ( b ) em B .