Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 9.Problemas - Ex. 92e

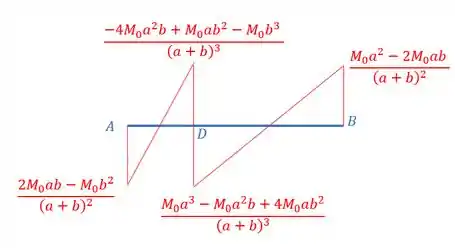
Determinar a reação em A e desenhar o diagrama de momento fletor para a viga com o carregamento mostrado.

Obs: determinação da reação em B e desenho do diagrama de momentos

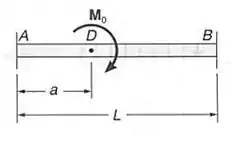
Passo 1

Podemos ir para a última parte que precisamos determinar o diagrama, como já sabemos a reação em A, vamos descobrir a reação em B. assim teremos que:

∑ F V = 0

M 0 b 2 + M 0 a 2 - 4 M 0 a b   a + b 3 - M 0 a + b + V B = 0

V B = M 0 a + b - M 0 b 2 + M 0 a 2 - 4 M 0 a b   a + b 3

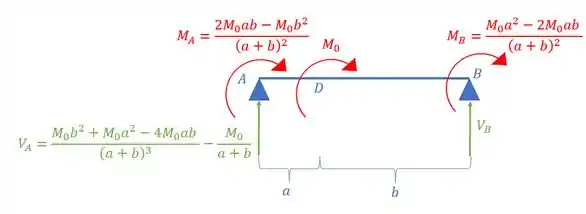
Passo 2

Para determinação do diagrama, precisamos ir ponto por ponto, assim teremos que:

  • Momento no ponto A e B

    • Sabe-se que o momento em A e B é concentrado e traciona as fibras da parte de baixo, assim, teremos que:

  • Momento no ponto D

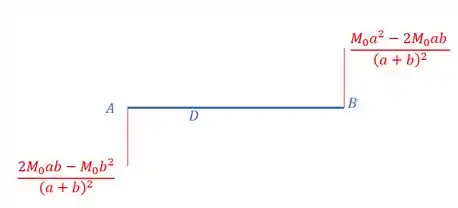
Para determinarmos o momento em D, precisamos analisar primeiro sem considerar o momento M 0 concentrado, e depois com o M 0 , assim, teremos que:

M D = M 0 b 2 + M 0 a 2 - 4 M 0 a b   a + b 3 - M 0 a + b a + 2 M 0 a b - M 0 b 2 a + b 2

M D = M 0 b 2 a + M 0 a 3 - 4 M 0 a 2 b   a + b 3 - M 0 a a + b + 2 M 0 a b - M 0 b 2 a + b 2

M D = M 0 b 2 a + M 0 a 3 - 4 M 0 a 2 b   a + b 3 - M 0 a a + b 2 a + b 3 + ( 2 M 0 a b - M 0 b 2 ) ( a + b ) a + b 3

Simplificando.

M D = M 0 b 2 a + M 0 a 3 - 4 M 0 a 2 b   a + b 3 - M 0 a ( a 2 + 2 a b + b 2 ) a + b 3 + ( 2 M 0 a b - M 0 b 2 ) ( a + b ) a + b 3

M D = M 0 b 2 a + M 0 a 3 - 4 M 0 a 2 b - M 0 a 3 - 2 M 0 a 2 b - M 0 a b 2 + 2 M 0 a 2 b + 2 M 0 a b 2 - M 0 a b 2 - M 0 b 3   a + b 3

M D = - 4 M 0 a 2 b + M 0 a b 2 - M 0 b 3   a + b 3

E como deu negativo, sabemos que traciona as fibras da parte de cima:

E como temos um momento concentrado, basta somarmos o momento concentrado no mesmo ponto:

M D = - 4 M 0 a 2 b + M 0 a b 2 - M 0 b 3   a + b 3 + M 0

M D = - 4 M 0 a 2 b + M 0 a b 2 - M 0 b 3 + M 0 a + b 3 a + b 3

M D = - 4 M 0 a 2 b + M 0 a b 2 - M 0 b 3 + M 0 ( a 3 + 3 a 2 b + 3 a b 2 + b 3 ) a + b 3

M D = - 4 M 0 a 2 b + M 0 a b 2 - M 0 b 3 + M 0 a 3 + 3 M 0 a 2 b + 3 M 0 a b 2 + M 0 b 3 a + b 3

Simplificando:

M D = M 0 a 3 - M 0 a 2 b + 4 M 0 a b 2 a + b 3

Como deu positivo, basta colocarmos ele pra baixo:

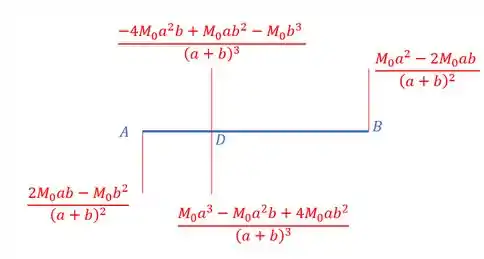
Como não temos cargas distribuídas, basta ligarmos esses momentos com uma reta, assim, teremos que o diagrama vai ser dado por:

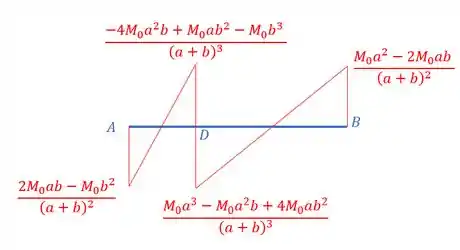
Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a linha elástica para a viga simplesmente apoiada utilizando a coordenada x onde 0 ≤ x ≤ L / 2 . Determine também a inclinação em A e a deflexão máxima da viga. E I é constante.
Podemos considerar que o tubo está apoiado em ambas extremidades por roletes e no centro por uma haste rígida C. A haste descansa sobre um cabo que está ligado aos apoios. Determine a força que deve s
Determine as equações da linha elástica utilizando as coordenadas x 1 e x 2 e especifique a inclinação em C e o deslocamento em B . E I é constante.
Uma haste delgada e flexível de 6 m de comprimento e 10 N/m D i g i t eae q u a ç ã oa q u i . çã de peso repousa sobre uma superfície lisa. Se uma força de 15N for aplicada a sua extremidade para lev
Determine a equação da linha elástica. Especifique as inclinações em A e B. EI é constante.