Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 11.Problemas - Ex. 124

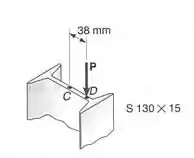
Um membro de aço comprimido, de 2,3m de comprimento efetivo, suporta uma carga excêntrica, como mostrado. Usando o método da tensão admissível, determinar a carga admissível P. Assumir E = 200 G P a   e   σ e = 250   M P a

Passo 1

E ai gurizada tudo belezinha? O enunciado pede que a gente determine a carga admissível P. Vem comigooo :D

Transição L r :     4,71 E σ γ

4,71 200 × 10 9 250 × 10 6 = 133,22

Consideremos os dados abaixo:

S 130 × 15 =     A = 1890 m m 2 = 1890 × 10 - 6 m 2

r m i n = r y = 16,3 m m = 16,3 × 10 - 3 m

S x = 79,8 × 10 3 m m 3 = 79,8 × 10 - 6 m 2

e x = 0

e y = 38   m m = 38 × 10 - 3 m

Passo 2

Consideramos a seguinte relação comprimento diâmetro, vem comigo :D

L e r m i n = 2 , 3 16,3 × 10 - 3 = 141,10 > 133,22

Determinando as tensões temos...

σ e = π 2 E L e r m i n 2 = π 2 200 × 10 9 141,10 2 = 99,14   M P a

σ μ = 0,377 σ e 1,67 = 0,877 99,14 1,67 = 52,06   M P a

P A + M x S x + M y S y = P A + P e y S x + P e x S y = P I A + e y S x + e x S y = K P

K P ≤ σ μ         P ≤ σ μ K

K = 1 1890 × 10 - 6 + 40 × 10 - 3 79,8 × 10 - 6 + 0 = 1,03035 × 10 3 m - 2

P ≤ 36,418 × 10 6 1,03035 × 10 3 = 35,3 × 10 2 N         P = 35,3 k N

Resposta

35,3 k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um membro de seção transversal retangular submetido à compressão, tem comprimento efetivo de 915mm e é feito da liga de alumínio 2014-T6, para a qual a tensão admissível é de 165 MPa. Usando o método
Resolver o prob. 144 assumindo que e= 5 mm
Um tubo retangular de aço é feito para suportar uma carga de 60kN, tendo uma excentricidade e=25mm. Os tubos disponíveis para o uso têm espessuras de parede que variam desde 6mm até 12mm, em increment
Uma coluna de madeira, de seção transversal retangular, tem um comprimento efetivo de 2,5m e deve suportar uma carga de 40kN, como mostrado. Usando o método da tensão admissível, projetar a coluna de
Resolver problema 148 selecionando o perfil laminado de aço de 250 mm de altura nominal