Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 12.Problemas - Ex. 24

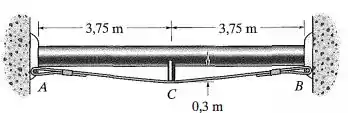
Podemos considerar que o tubo está apoiado em ambas extremidades por roletes e no centro por uma haste rígida C. A haste descansa sobre um cabo que está ligado aos apoios. Determine a força que deve ser desenvolvida no cabo, se a haste impedir que o tubo ceda ou sofra deflexão no centro. O tubo e o fluido dentro dele têm um peso combinado de 2 kN/m. EI é constante.

Passo 1

Para 0 ≤ x ≤ 3,75   m :

∑ M = 0 M x - P x + 2 x ( 0,5 x )   = 0 M x = P x - x 2

Sabemos que:

E I d 2 v 1 d x 1 ² = M x

Logo:

E I d 2 v 1 d x 1 2 = P x - x 2

E I d v 1 d x 1 = P 2 x 2 - x 3 3 +   C 1

E I v 1 = P 6 x 2 - x 4 12 + C 1 x + C 2

Passo 2

As condições de contorno serão:

x = 0 → v = 0

x = 3,75   m → v = 0

Logo, substituindo:

C 2 = 0

2,34375 P - 4,39453 + C 1 = 7,03125 P - 17,578125 + C 1 P = 2,8125   k N

Passo 3

Por fim, devemos fazer um somatório das forças:

∑ F y = 0 2 × 2,8125 - 15 + F = 0 F = 9,375   k   N

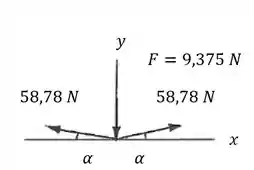
E então, substituindo: sin ⁡ α = 0,0797452 2 T c a b o sin ⁡ α - 9,375 = 0 T c a b o = 58,78   k N

Resposta

T c a b o = 58,78   k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma barra uniforme A E está apoiada em dois pontos B e D . Determine a distância a das extremidades da barra até os apoios, para que as deflexões em A ,CeE sejam iguais e para baixo.
Para a viga prismática com o carregamento mostrado, determinar:A declividade no ponto AA deflexão no ponto D.
Para a viga com o carregamento mostrado, determinar:O valor de P para que a deflexão seja zero na extremidade A da viga;A variação dos valores de P , para que o valor absoluto da deflexão na extremida
Para a viga uniforme em balanço, com o carregamento mostrado, determinar: ( a ) a declividade da extremidade livre; ( b ) a deflexão da extremidade livre.
Para a viga prismática com o carregamento mostrado, determinar: ( a ) a declividade no ponto A ; ( b ) a deflexão no ponto D .