Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 4.Problemas - Ex. 28
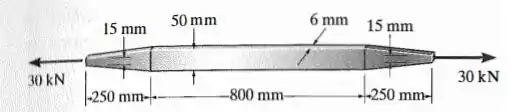
Determine o alongamento da tira de alumínio quando submetida a uma força axial de .
Passo 1
Faaaala, querido! Cê tá bem?
Então, ele quer saber o alongamento dessa tira por causa de uma força axial . Normalmente quando a gente quer alongamento devido a uma força, a gente usa essa fórmulinha:
Só que , que é a área transversal da peça, é constante apenas no meio. Nas extremidades ela varia, porque a tira vai se afinando, sabe?
Então a gente vai dividir nossa peça em duas. A primeira parte é esse meio que tem constante. Aí vai ser dado pela fórmula acima.
E as extremidades? Cara, como elas como elas estão com variando, vamos precisar uma fórmulinha diferenciada para . Essa aqui:
Ou seja, se varia, ela é uma função. Então a gente usa uma integral! Percebe que as fórmulas são parecidas. A diferença é que em vez de multiplicar o termo por , a gente integral ele de a . Bora então ver como usar essas fórmulinhas!
Passo 2
Então, vamos começar por :
é a área retangular da parte central da tira, dada por:
Substituindo esse valor e o outros dados:
Passo 3
Agora vamos olhar para as extremidades. Percebe que elas são simétricas em relação ao meio da tira. Então a deformação de uma ponta é igual a deformação da outra ponta.
Então o que a gente vai fazer calcular a deformação de uma ponta e multiplicar por 2, ok?
Aí vimos que nossa área varia né? Então a primeira coisa a fazer é achar uma função que descreve essa variação. Percebe que só a altura da área transversal varia, a largura permanece . Então vamos achar uma função para a altura dessa tira na extremidade.
Vamos colocar um eixo começando na ponta esquerda da tira
Em , temos , e em , temos . A mudança de altura é linear (porque temos esse formato composto por retas), então vamos usar a expressão de função linear e os nossos dados, e achar :
Para e :
Para , e :
Logo, nossa função fica:
Passo 4
A gente já tem a função altura. Para achar a função área , a gente multiplica a altura pela largura :
Aí usamos a nossa fórmulinha do alongamento:
Lembra que esse 2 é porque estamos usando a simetria da peça, porque as deformações nas extremidades serão iguais porque elas são iguais. Substituindo nossos dados:
Percebe que a gente integrou de a , porque nossa peça está nesse intervalo de (considerando o eixo que a gente escolheu.
Passo 5
Vamos tirar o que é constante da integral:
Fazendo uma substituição do tipo , podemos resolver essa integral:
Calculando:
Logo, o alongamento total da tira é: