O suporte é mantido preso à parede por três parafusos de aço em , e . Cada parafuso tem diâmetro de e comprimento de quando não alongado. Se uma força de for aplicada ao suporte como mostra a figura, determine a força desenvolvida em cada parafuso. Para o cálculo, considere que os parafusos não sofrem cisalhamento; ao contrário, a força vertical de é suportada pela saliência em . Considere também que a parede e o suporte são rígidos. O detalhe mostra a deformação muito ampliada dos parafusos.

Se queremos descobrir forças, precisamos do diagrama de corpo livre.

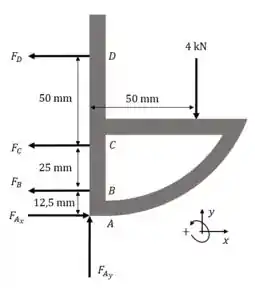
Vamos fazer o equilíbrio de momentos no ponto , assim não precisamos nos preocupar com e .

Poderíamos checar o equilíbrio de forças também, mas não vai ajudar porque só vai introduzir as incógnitas e no problema

Temos três incógnitas e uma equação. Precisamos de mais relações que envolvam apenas essas forças.

A barra vai girar ao redor da saliência em . Como ela é rígida, ela não se deforma. Vamos ver como os deslocamentos dos parafusos se relacionam. Na figura abaixo, só a parte reta vertical do suporte está desenhada (linha preta).

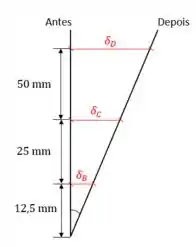
Há três triângulos nessa figura com um ângulo em comum. Primeiro, vamos usar a tangente do ângulo olhando para o triângulo intermediário e o menor:

Vejamos agora a tangente do ângulo olhando o triângulo maior e o menor.

Agora que sabemos como os deslocamentos dos parafusos estão relacionados, podemos usar a relação carga-deslocamento para checar as forças:

Finalmente temos três equações relacionado as forças! Usando e obtemos