Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 4.Problemas - Ex. 63
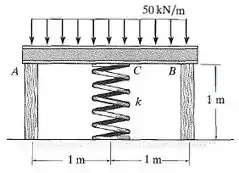
A barra rígida é apoiada pelos dois postes curtos de pinho branco e uma mola. Se o comprimento dos postes quando não carregados for e a área de seção transversal for e a mola tiver rigidez e comprimento quando não deformada, determine a força em cada poste após a aplicação da carga à barra.
Passo 1
Fala! Vamos entender a situação.
Uma barra rígida tem como suporte dois postes de pinho branco (espruce branco) e uma mola. Um carregamento distribuído é colocado sobre a barra
Características dos postes em e :
- Pinho branco (espruce branco): (Tabelado)
- Área: .
- Comprimento inicial: .
Características da mola:
- Rigidez: .
- Comprimento quando livre:
O carregamento de é distribuído linearmente ao longo de sobre a barra.
É importante notar já de cara que o comprimento dos postes é menor que o comprimento livre da mola já antes do carregamento ser aplicado.
Isso significa que a mola já vai estar exercendo uma força por causa dessa compressão, além de outras deformações que podemos achar.
Queremos a força exercida em cada poste.
Passo 2
Estamos procurando por forças, então comecemos com o diagrama de corpo livre.
Há uma simetria do diagrama em relação a . Fazendo o equilíbrio de momentos nesse ponto:
Show! Agora o equilíbrio de forças na vertical:
A força é desenvolvida por uma mola de rigidez . Se substituirmos a relação linear de uma mola na última equação, chegamos em
Atenção que nessa equação a variável significa a compressão total que a mola sofre em relação ao seu comprimento livre de , depois do carregamento.
Temos uma equação e duas incógnitas ( e ). Precisamos de mais uma equação.
Passo 3
Primeiro temos que lembrar que a mola já começa comprimida desde o início do problema. Depois disso, como a barra é rígida e há simetria, ela não vai poder encurvar, fazendo ago assim:
Com isso, a compressão adicional da mola precisa ser igual ao deslocamento dos postes. Vamos escrever isso:
Enfatizando: a compressão total da mola é (antes do carregamento) mais o deslocamento dos postes (deformação após carregamento).
Passo 4
A partir daqui é tudo fácil! Usamos a fórmula da relação carga-deslocamento para o poste!
Substitua o que encontramos para em para acabar
E como :
Resposta
Força nos postes em e em :.