Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 4.Problemas - Ex. 56
A barra está presa por um pino em e é sustentada por duas hastes de alumínio, cada uma com diâmetro de e módulo de elasticidade . Considerando que a barra é rígida e inicialmente vertical, determine o deslocamento da extremidade quando for aplicada uma força de .
Passo 1
Uma barra vertical rígida está presa a duas hastes em e , e a um pino em .
Características das hastes e :
- Alumínio: .
- Diâmetro: .
- Comprimento inicial: e
Uma força horizontal de puxa a barra para a direita bem no meio dela. A barra rígida vai girar ao redor do pino em .
Queremos saber o quanto a extremidade se move, .
Passo 2
A barra vai girar ao redor do pino em . Como ela é rígida, ela não se deforma. Vamos ver como os deslocamentos das hastes se relacionam. A barra é a linha preta na figura.
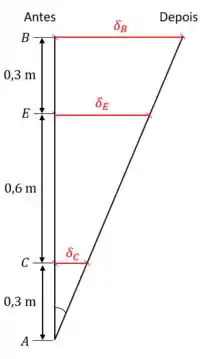
Lembrando que queremos calcular , vamos relacionar isso com o deslocamento de alguma haste. Na figura temos três triângulos com um ângulo em comum. Olhando pra dois deles, podemos formar uma equação com a tangente do ângulo:
Pronto, se acharmos o problema acabou. Vamos precisar da fórmula da relação carga-deslocamento
A área da haste a gente consegue calcular, e sabemos e . Então pra achar só nos falta achar .
Passo 3
Se estamos procurando uma força, fazemos o diagrama de corpo livre. Só as reações horizontais nos interessam aqui.
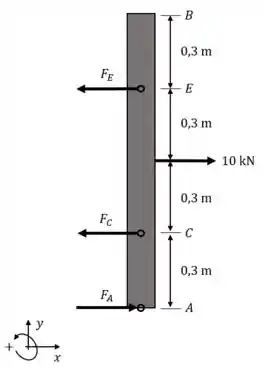
Vamos fazer o equilíbrio de momentos no ponto , assim a força não contribui.
Precisamos de outra equação que relacione apenas essas forças.
Passo 4
Volte na figura do Passo 2. Vamos usar a tangente do ângulo de novo, agora para relacionar as forças e . Olhando pro triângulo intermediário e pro menor, temos
E usando a fórmula da relação carga-deslocamento:
Substitua os valores para achar:
Passo 5
Use em para obter
Agora podemos calcular .
A área haste é . Então
Passo 6
Pela relação que achamos no Passo 2:
Resposta
Deslocamento da extremidade :