Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 3.Problemas - Ex. 68
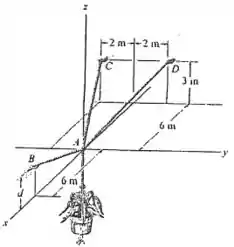
Determine a altura d do cabo AB, de modo que a força nos cabos AD e AC sejam a metade da força no cabo AB. Qual é a força em cada cabo para esse caso? O vaso de planta tem uma massa de .
Passo 1
Fala galera boa, sei que a questão pode assustar um pouco mas fica tranquilo vamos facilitar ela ao máximo juntos, tá?
A gente vai precisar transformar as forças em vetores, para que possamos aplicar os somatórios de forças e enfim encontrar o valor de cada uma delas.
Lembrando que a notação vetorial funciona da seguinte forma:
Onde x, y e z são as distâncias cotadas na figura pra cada força nos seus respectivos eixos.
Tem-se que o vaso exerce uma força peso para baixo que tem intensidade de .
O enunciado nos diz que as forças em AC e AD, devem ser metade da força em AB, sendo assim:
Para :
E para :
Passo 2
Logo, fazendo o diagrama de corpo livre tem-se:
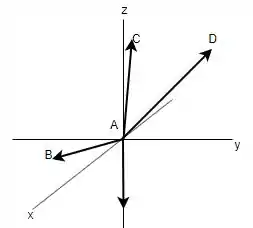
E, então, observando o desenho feito consegue-se montar as equações de equilíbrio.
Passo 3
O equilíbrio requer quer que o somatório de forças em cada dimensão seja nulo, ou seja:
Adotando o sentido dos eixos mostrado no desenho do enunciado:
No entanto, a partir das equações (1) e (3):
Passo 4
Lembrando que , então:
Logo,
Passo 5
Para determinar a altura d, pode-se fazer uma relação trigonométrica já que AB forma um ângulo com o eixo x. Logo, chamando esse ângulo de :
Tendo que
Então:
Portanto: