Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 7.Problemas - Ex. 49
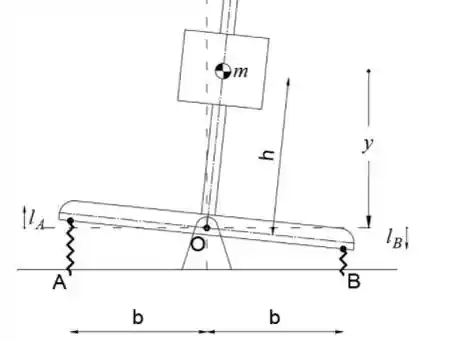
Determine a altura máxima h da massa m para a qual o pêndulo invertido será estável na posição vertical mostrada. Cada uma das molas tem uma rigidez k, e elas têm pré-compressão iguais nesta posição. Despreze a massa do restante do mecanismo.
Passo 1
Primeiro, vamos desenhar o diagrama de força ativa
Observe que há força P agindo no sistema, há também uma mola acoplada e que a massa é desprezada. Sabendo disso, podemos escrever a equação de equilíbrio
(1)
Veremos no esboço que a distância y é
Passo 2
Expressão para energia potencial gravitacional
Substituiremos
Derivaremos ambos lados da equação
(2)
Passo 3
Uma vez que existem duas molas ligadas ao sistema, a expressão da energia potencial elástica é
Uma vez que , escreveremos a equação acima como
Derivaremos ambos lados da equação
(3)
Passo 4
A seguir, substituiremos δVg e δVe pelas expressões (2) e (3) na equação de equilíbrio (1)
Observe que o sistema é estável quando a segunda derivada da equação de equilíbrio é maior que zero
(4)
Para verificar a estabilidade da posição θ = 0, vamos simplesmente colocar o valor de θ em (4)
Podemos expressar a altura h como