Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 7.Problemas - Ex. 14
Ao projetar a prensa de alternância mostrada, n voltas do eixo sem-fim A seriam necessárias para produzir uma volta das rodas sem-fim B que operam as manivelas BD. O aríete móvel tem massa m. Despreze qualquer atrito e determine o torque M no eixo sem-fim necessário para gerar uma força compressiva C na prensa para a posição θ = 90 ∘. (Observe que os deslocamentos virtuais do aríete e do ponto D são iguais para a posição θ = 90 ∘.)
Passo 1
Primeiro, vamos desenhar o diagrama de força ativa
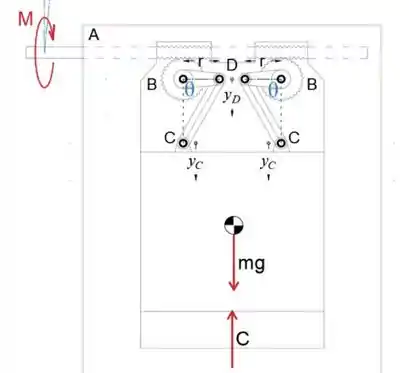
Uma vez que sabemos que leva n voltas do eixo A para fazer uma volta em B. é claro que o ângulo α é n vezes maior que o ângulo θ
Derive ambos lados da equação
Comprimento dp membro é , para rotação do ângulo θ movimento virtual do ponto D é
Como os movimentos virtuais dos pontos D e C (ram com peso mg) são iguais para θ = 90 ∘, podemos escrever yC como
Mudança infinitesimal na posição do carneiro é
Passo 2
O Trabalho Virtual realizado pelo casal M é produto da Rotação Virtual \ deltaa e momento que a força produz
Substitua por
(1)
Podemos Trabalho Virtual feito pelas forças mg e C como
Substituiremos por
(2)
Passo 3
A seguir, vamos aplicar o Princípio do Trabalho Virtual, que afirma que a soma do trabalho realizado por todas as forças ativas é igual a zero
Substituiremos e pelas expressões e respectivamente
Dividiremos ambos lados da equação por
A partir daqui expressaremos como
Por fim, substituiremos por seu valor