Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 11.Problemas - Ex. 6

O cabo de reboque exerce uma força P = 6   k N na extremidade da lança do guindaste de 8   m de comprimento. Se x = 10   m , determine a posição θ da lança para que essa força crie um momento máximo em relação ao ponto O . Qual é esse momento?

Passo 1

Oi pessoal? Vamos para mais um exercício?

Este exercício é bem semelhante ao anterior. Porém, agora temos o valor de x e queremos o ângulo θ para obter o momento máximo.

Observe o diagrama abaixo:

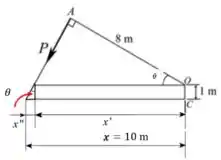
O momento é máximo quando P fica perpendicular à lança do guindaste de 8     m . Deve-se atentar que a lança está 1     m acima do chão, por isso temos que calcular x ' ' .

Fazendo então uma análise geométrica, temos que:

x = x ' + x ' '

Temos que x ' = 8 cos ⁡ θ e x ' ' = 1 tan ⁡ θ . Logo:

x = 8 cos ⁡ θ + tan ⁡ θ

Como x = 10 , temos que:

10 = 8 cos ⁡ θ + tan ⁡ θ

Passo 2

Desenvolvendo, temos que:

10 = 8 cos ⁡ θ + sen ⁡ θ cos ⁡ θ

10 cos ⁡ θ - 8 = sen ⁡ θ

Elevando os dois lados ao quadrado, temos que:

100 cos 2 ⁡ θ - 2 ⋅ 10 cos ⁡ θ ⋅ 8 + 8 2 = sen 2 ⁡ θ

Sabemos que o sen 2 ⁡ θ = 1 - cos 2 ⁡ θ , portanto:

100 cos 2 ⁡ θ - 80 cos ⁡ θ + 64 = 1 - cos 2 ⁡ θ

101 cos 2 ⁡ θ - 80 cos ⁡ θ + 63 = 0

Resolvendo por baskara, temos que:

cos ⁡ θ = - - 80 ± - 80 2 - 4 101 63 2 101

Resolvendo, temos que:

cos ⁡ θ = 0,85227   o u   0,73188

O que nos daria:

θ 1 = cos - 1 ⁡ 0,85227

θ 1 = 31,54 °

E:

θ 2 = cos - 1 ⁡ 0,73188

θ 2 = 42,955 °

Passo 3

O momento máximo será:

↺ + ∑ M O = M O M á x

M O M á x = ( 6   k N ) ( 8   m )

M O M á x = 48   k N ⋅ m ↺

Resposta

θ 1 = 31,54 °

θ 2 = 42,955 °

M O M á x = 48   k N ⋅ m ↺

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine os valores de equilíbrio de θ e a estabilidade do equilíbrio em cada posição para a roda não balanceada sobre a rampa de 10°. O atrito estático é suficiente para prevenir deslizamento. O cen
Determine a intensidade da força P exigida para manter a barra lisa de 50 kg em equilíbrio com θ = 60 ° .
O mecanismo está sujeito a uma força P = 2 kN. Determine o ângulo θ para o equilíbrio. A mola está livre quando θ = 0 ° . Despreze a massa dos membros.
Determine a intensidade exigida da força P para manter o equilíbrio do mecanismo em θ = 60 ° . Cada membro tem uma massa de 20 kg.
A ponte de 2 Mg, com centro de massa no ponto G, é levantada pelas duas vigas CD, localizadas em cada lado da ponte. Se o contrapeso E de 2 Mg estiver conectado às vigas como mostrado, determine o âng