Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 1.9 - Ex. 1

Determine os ângulos feitos pelo vetor V = - 36   i + 15   j com o eixo positivo dos x e dos y . Escreva o vetor unitário n na direção de V .

Passo 1

Pessoal que tal começarmos esse problema fazendo um desenho de como é esse vetor V parece bacana, né? Para isso a gente precisa lembrar que i ^ é o vetor unitário em x e j ^ o vetor unitário em y . Então vai ficar assim:

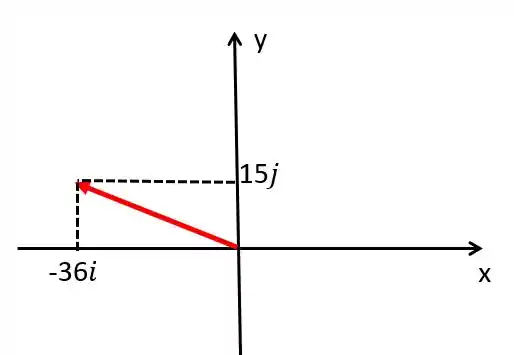
Passo 2

Galera, vamos escrever o ângulo feito entre V e o eixo positivo dos x como θ x , e o ângulo feito entre   V e o eixo positivo dos y como θ y .

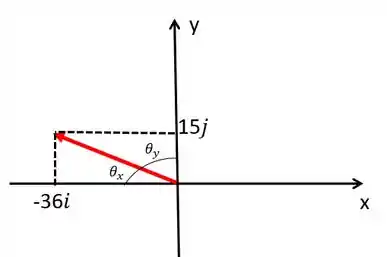
Dessa forma e observando a geometria da figura a gente vai ver que:

cos ⁡ θ x = V x V                     e                   cos ⁡ θ y = V y V

Onde V x = - 36 e V y = 15 , então só falta calcular o módulo V :

V = V x 2 + V y 2

V = - 36 2 + 15 2

V = 39

Passo 3

Beleza! Sabendo o módulo V do vetor V , podemos enfim determinar os ângulos θ x e θ y :

cos ⁡ θ x = - 36 39

θ x = arcos ⁡ - 12 13

θ x = 157,4 °

E

cos ⁡ θ y = 15 39

θ y = arcos ⁡ 5 13

θ y = 67,4 °

Passo 4

Agora vamos lembrar o que é o vetor unitário de um vetor, qualquer. É aquele que tem a mesma direção e sentido prém seu módulo vale 1, representado graficamente fica assim, onde a setinha preta é o vetor unitário:

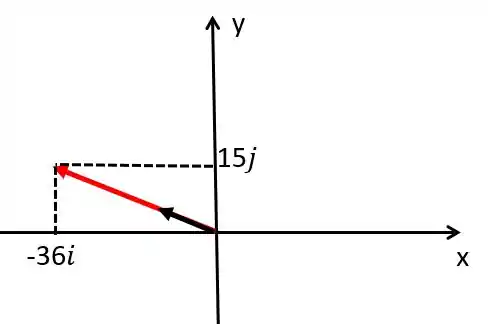
Para escrever o vetor unitário n na direção de V , a gente só precisa dividir o vetor V pelo seu módulo:

n = V V

n = - 36   i + 15   j 39

n = - 36   i 39 + 15   j 39

n = - 0,923   i + 0,385   j

Resposta

θ x = 157,4 °

θ y = 67,4 °

n = - 0,923   i + 0,385   j

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

2.22. Se Φ = 30 ° , F 1 = 5k N e a força resultante deve ser orientada ao longo do eixo y positivo, determine a intensidade da força resultante, se F 2 necessita ser mínima. Além disso, quais valores
2.24. Se a força resultante F R está orientada ao longo da linha a 75° no sentido horário a partir do eixo x positivo e a intensidade de F 2 deve ser mínima, determine as intensidades de F R e F 2 , e
2.23. Se θ = 30 ° , F 2 = 6k N , determine a intensidade da força resultante que atua sobre a chapa e sua direção, medida no sentido horário a partir do eixo x positivo.
Duas forças são aplicadas a um suporte tipo gancho indicadas na figura. Usando trigonometria e sabendo que a intensidade de P é 35N , determine (a) o ângulo requerido a se a resultante R das duas forç
Resolva o problema 2.2 usando trigonometria.