Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.10 - Ex. 209
Determine a área da superfície curva do sólido de revolução mostrado.
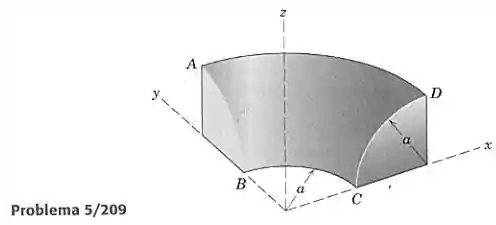
Passo 1
A área de uma superfície de revolução em torno de um eixo é dada por:
Onde é o comprimento da linha que é revolucionada e é o “raio médio”, ou seja, a coordenada do centroide da linha (se considerarmos a linha desenhada no plano e que vai girar em torno de ). Nossa figura que é revolucionada é um quarto de circunferência, que tem a distância do centro de massa (horizontal e vertical) até o centro conhecida e igual a
Como temos só um quarto da revolução inteira, então na verdade nossa fórmula fica:
Passo 2
Primeiro vamos calcular o comprimento do arco:
Agora vamos achar , olhando o desenho:
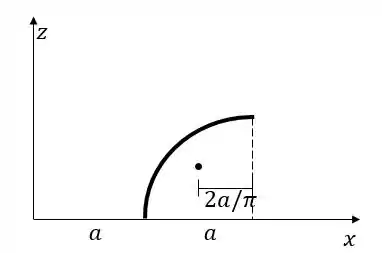
Passo 3
Então calculamos a área:
Resposta
Exercícios de Livros Relacionados
O trocador de calor irradia energia térmica a uma taxa de 2500k J / h para cada metro quadrado de sua área superficial. Determine quantos joules ( J ) são irradiados dentro de um período de 5 horas.
Determine a altura h à qual o líquido deve ser vertido dentro do copo cônico de modo que atinja três quartos da área de superfície no interior do copo. Para o cálculo, desconsidere a espessura do copo
A corrente da esquerda para a direita no fluxo causa um arrasto uniforme de 4 lb por pé do fluxo cruzado no cabo flutuante que é conectado aos postes A e B. Determine as tensões mínimas e máximas no c
Um rebocador motorizado reboca uma barcaça com um cabo que tem uma massa de 14 kg por metro de comprimento. Observa-se que a tangente ao cabo no ponto A é horizontal. Determine as tensões em A e B.
Um cabo pesando 25 newtons por metro de comprimento é suspenso do ponto A e passa sobre a pequena polia em B. Calcule a massa m do cilindro acoplado que produzirá o afundamento de 9 m. Determine també