Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 16

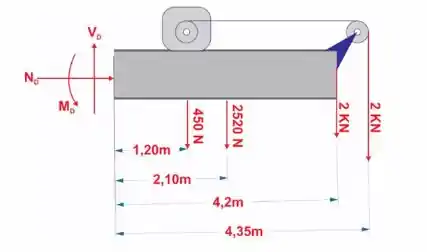
Determine as cargas internas resultantes que agem na seção transversal que passa pelos pontos C e D da viga no Problema 1.15.

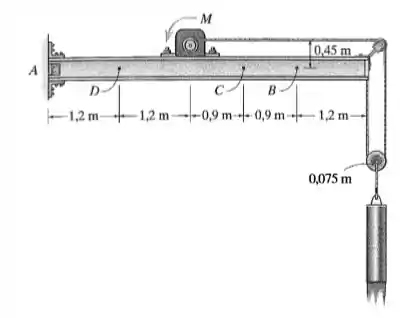
Passo 1

Em um primeiro passo, vamos fazer o DCL

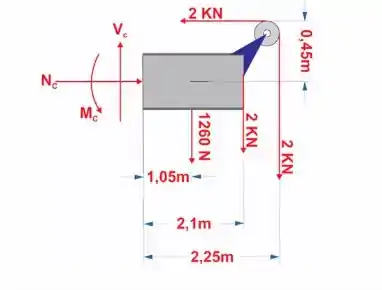
Onde V C → Força cortante em C

                    M C → Momento

                    N C → Força normal

Passo 2

Agora é só utilizarmos as equações de equilíbrio e momento em relação a C

∑ F x = 0 N C = 2   k N

∑ F y = 0 V C = 5,26   k N

∑ M C = 0 M C + 2 × 0,45 = 1,26 × 1,05 + 2 × 2,1 + 2 × 2,25 M C = 9,123   k N . m

Passo 3

Para D, é só repetirmos os passos anteriores

∑ F x = 0 N D = 0

∑ F y = 0 V D = 6,97   k N

∑ M D = 0 M D = + 1,2 × 0,45 + 2,52 × 2,1 + 2 × 4,2 + 2 × 4,35 M D = 22,932   k N . m

Resposta

N C = 2   k N

V C = 5,26   k N

M C = 9,123   k N . m

N D = 0

V D = 6,97   k N

M D = 22,932   k N . m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A estrutura do poste de energia elétrica suporta os três cabos, e cada um deles exerce uma força de 4k N nas escoras. Se as escoras estiverem acopladas por pinos em A , B e C , determine as cargas int
Determine as cargas internas resultantes que agem na seção transversal que passa pelo ponto B .
A carga de 4.000N está sendo levantada a uma velocidade constante pelo motor M, que pesa 450N . Determine as cargas internas resultantes que agem na seção transversal que passa pelo ponto B na viga. A
Determine a resultante das forças internas normal e de cisalhamento no elemento na seção b - b , cada uma em função de θ . Represente esses resultados em gráficos para 0 ≤ θ ≤ 90 ° . A carga de 650N é