Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 15
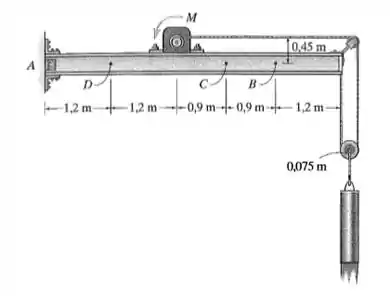
A carga de está sendo levantada a uma velocidade constante pelo motor M, que pesa . Determine as cargas internas resultantes que agem na seção transversal que passa pelo ponto B na viga. A viga pesa e está fixada à parede em .
Passo 1
Falaa, meu querido! Queremos os esforços internos na seção em . Vamos entender o que está acontecendo nessa viga.
Ele diz que ela possui um peso de . Isso pode ser interpretado como uma carga distribuída ao longo de toda a viga. E o motor pesa , o que é uma carga concentrada.
Agora vamos entender a roldana. Essas duas cordinhas puxando o peso dividem a carga de entre si, ficando para cada.
A corda direita está passando pela roldana e está ligada ao motor. Ela trasmite a viga as forças de tensão na corda pela roldana. Então nossa viga fica sujeita a uma força na horizontal no sentido do motor e uma força vertical no sentido do pesinho.
A cordinha da esquerda só está ligada na viga diretamente e ela transmite uma força para baixo de . Fazendo um esboço disso, nossa viga, que é engastada, está assim:
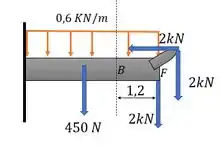
Aí a gente precisa achar os esforços internos em . Bora lá!
Passo 2
A ideia para achar esforços internos em uma seção é que a gente pode cortar nossa viga nessa seção e escolher um dos pedaços.
No nosso caso, podemos escolher o lado da esquerda, aí não precisamos achar as reações no engaste. E aí, colocamos as componentes dos esforços internos nessa seção e achamos seus valores pela equação de equilíbrio, ok?
Só para facilitar, essa carga distribuída no trecho que a gente representou no desenho pode ser substituída por uma carga concentrada em
Em relação a . E de valor
Vamos fazer o DCL disso
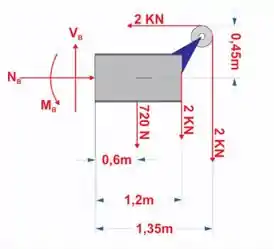
Onde Força cortante em B
Momento
Força normal
Passo 3
Agora é só utilizarmos as equações de equilíbrio e momento
Obs: alguns sinais ficaram diferentes do gabarito pela escolha de sentido das componentes no DCL. As duas respostas são válidas visto que nesse capítulo o autor não apresentou ainda a convenção de sinais para esses esforços, ok?