Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 4.Problemas - Ex. 41
O apoio é composto por um poste sólido de latão vermelho C83400 embutido em um tubo de aço inoxidável 304. Antes da aplicação da carga, a folga entre essas duas partes é . Dadas as dimensões mostradas na figura, determine a maior carga axial que pode ser aplicada à tampa rígida A sem provocar o escoamento de qualquer um dos materiais.
Passo 1
Falaa!
Antes de começar, as propriedade desses materiais que ele deu são tabeladas, tá? Então a tensão de escoamento e o módulo de elasticidade que usarmos aqui vêm de tabelinhas de propriedades desses materiais.
Agora sim, vamos entender a situação do nosso problema. Temos um tubo de aço, e dentro dele um poste de latão. Eles dois juntos precisam suportar a força na tampa rígida. Queremos o maior valor de que não cause escoamento em ninguém.
Mas atenção: isso só acontece se o latão conseguir sofrer uma compressão que cause uma contração de sem escoar. Só depois disso, que temos os dois materiais resistindo a , pois aí que o aço começa a encostar na tampa também.
Então, antes de continuar o rolê, precisamos ver se o latão não escoa por causa de até que a tampa encoste no aço, ou seja, até a gente atingir:
Então vamos achar o valor de quando o latão está na tensão de escoamento, e ver se o resultado é menor ou maior que . Temos que aplicar a fórmula de :
Temos que
Podemos achar em função de pela fórmula da tensão média:
Voltando para a deformação:
Então, beleza, o alongamento que ele tem no escoamento é de , que é menor que . Então o latão consegue passar do alongamento de sem escoar. Vamos seguir.
Passo 2
Então nosso DCL de quando os dois materiais estão encostando na tampa fica:
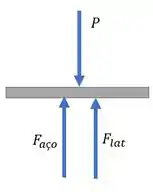
Onde é a reação gerada pelo tubo de aço e a reação do poste de latão.
A gente quer descobrir o maior valor de para que nenhum desses materais sofram escoamento.
Então o que a gente precisa fazer é achar as reações em cada um desses elementos e a partir disso achar uma expressão para a tensão normal neles em função de . E aí depois é comparar esses valores com a tensão de escoamento para cada material para achar . Bora!
Passo 3
Precisamos achar esses valores de em função de . Com isso, podemos utilizar a fórmula do equilíbrio no eixo :
Repara que temos duas icógnitas, mas só uma equação. A gente precisa de mais uma, certo?
Passo 4
Vamos tentar achar essa equação que falta da compatibilidade de deslocamentos. Inicialmente nossa barra está encostada só no latão e distante de 1 mm da parte de aço.
Já que é rígida (não se encurva), no momento onde temos um carregamento máximo, podemos supor que estará encostada nos dois materiais, e causando compressão nos dois.
Nesse momento, a carga age sobre essa “tampa” do poste. Essa tampa não se deforma né? Porque ela é rígida. Então, se não há deformação, ela permance reta sempre. Logo, a altura que ela desce no meio, ela desce igualmente nas extremidades. Temos algo assim:
Dessa figura, tiramos que o encurtamento do aço é igual ao encurtamento do latão menos . Isso porque antes de começarem a se defomarem juntos, o latão já havia se encurtado de , lembra? Nossa equação fica:
Agora, temos que aplicar a fórmula de para cada um:
Repare que virou porque passamos para metro!
Essa é nossa segunda equação.
Passo 5
Agora, achamos as em função de pelo sisteminha de suas equações:
Resolvendo ele, achamos:
Passo 6
E agora, achamos a tensão para cada material e comparamos com a tensão admissível. O menor é o que a gente escolhe.
Os valores de tensão admissível são tabelados.
Para o aço:
Para o latão:
Obs: Essa questão está bem diferente do gabarito. Pode ser algum erro de tradução que deixou os dados errados. Mas se cair uma parecida na sua prova, segue esse passo a passo, que dá bom! 😉