Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 20
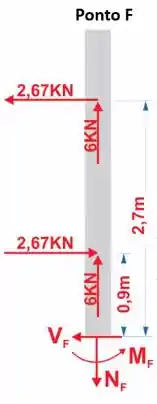
A estrutura do poste de energia elétrica suporta os três cabos, e cada um deles exerce uma força de nas escoras. Se as escoras estiverem acopladas por pinos em , e , determine as cargas internas resultantes nas seções transversais que passam pelos pontos , e .
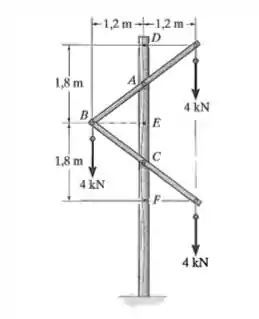
Passo 1
Em um primeiro passo, vamos fazer o DCL
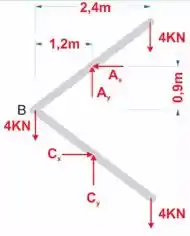
Passo 2
Agora é só utilizarmos as equações de equilíbrio e momento
Passo 3
Novamente, vamos usar o DCL para as estruturas superior e inferior para calcularmos as forças restantes
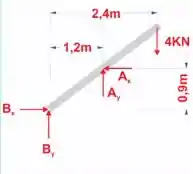
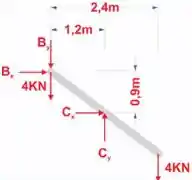
Passo 4
Por fim, traçamos um corte em D e fazemos o DCL para utilizar as equações do equilíbrio.
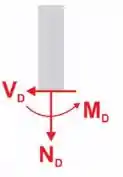
Passo 5
Agora é só repetirmos o último passo para o pontos e e correr pro abraço.
Para o ponto
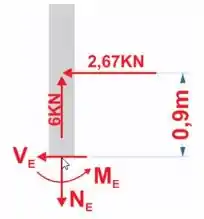
Para :
Resposta
Exercícios de Livros Relacionados
Determine o módulo da seção plástica e o fator de forma para a viga em I .
A coluna é construída de concreto de alta resistência e seis hastes de reforço de aço A-36. Se for submetida a uma força axial de 150 kN, determine o diâmetro exigido para cada haste, de modo que 1/4
Considere o problema geral de uma viga simplesmente apoiada submetida a n cargas concentras. Escreva um código computacional que possa ser usado para determinar a força cortante interna e o momento em
Faça os diagramas de força cortante e momento fletor para a viga e determine a força cortante e o momento fletor na viga em função de x, onde 0 ≤ x ≤ 1,8m
A viga é feita de um poliéster cuja curva tensão-deformação e mostrada na figura. Se a curva puder ser representada pela equação σ = 140 tg-1(15ε) MPa, onde tg-1(15ε) é dada em radianos, determine o v