Determine as cargas internas resultantes que agem na seção transversal que passa pelo ponto .
Passo 1
Oláaaa, querido! Tá bem?
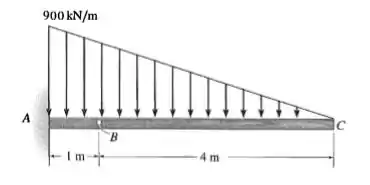
Então, ele quer saber as cargas internas que atuam na seção que passa por . Para fazer esse tipo de questão, a primeira coisa é cortar nossa peça na seção que ele pediu, escolher um lado e fazer o diagrama de corpo livre da situação nova.
A gente escolhe o lado que não tem apoio. Percebe que o lado esquerdo tem o apoio, a gente não sabe as reações nesse apoio, então falta uma informação desse lado. Já o lado esquerdo não tem apoio, logo vai ser melhor usar ele.
Então vamos cortar nossa estrutura em olhar só para cima. Assim:
Aí a gente posiciona na seção as nossas cargas que queremos calcular.
Passo 2
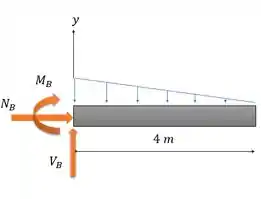
Fofo, né? Mas repara que a gente não sabe o valor da altura do triângulo azul, isso porque a gente cortou o triângulo maior de altura , lembra? Então a gente precisa descobrir essa altura nova. Vamos usar semelhança de triângulos.
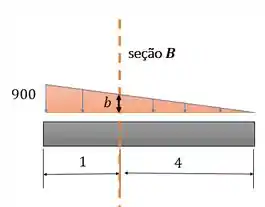
Daí o diagrama completo fica:
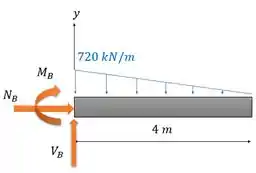
Passo 3
Agora vamos achar nossas cargas.
Para isso, a gente precisa achar a força concentrada equivalente a esse carregamento distribuído, tá bem? Ele tem a cara triângulo.
A força resultante para a carga em formato de triângulo vai ter o valor da área do triângulo
E o ponto de ação dela está na linha que passa pelo centroide do triângulo. Ele está localizado a um terço da ponta do triângulo, então nossa força está em
Nosso sistema fica:
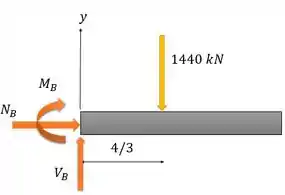
Passo 4
Agora é utilizarmos as equações de equilíbrio e momento para achar as cargas:
E para o momento, considerando o sentido horário positivo: