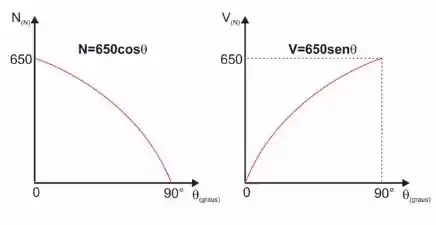
Determine a resultante das forças internas normal e de cisalhamento no elemento na seção , cada uma em função de . Represente esses resultados em gráficos para A carga de é aplicada ao longo do eixo do centroide do elemento.
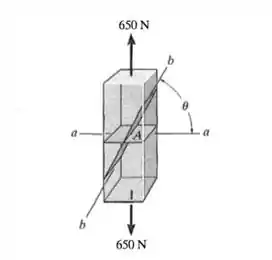
Passo 1
Fazendo o DCL temos que
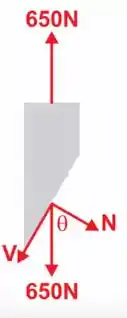
Passo 2
Para a seção é utilizar as equações do equilibrio, decompondo o par de reação da força de 650 N que age na seção. Fica assim:
Passo 3
Agora fica mole esboçar o gráfico. É só observar que temos uma cossenoide para e uma senoide para
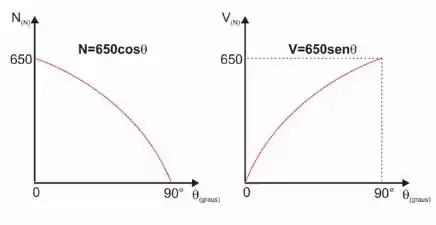
Resposta