Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 9.Problemas fundamentais - Ex. 12

Determine o centro de massa ( x - , y - , z - ) do bloco sólido homogêneo.

Passo 1

A gente tem que pensar sempre na divisão mais natural a se fazer. Aqui, o que me parece razoável é dividir nesse “retângulo” e nos dois “triângulos”. Para as partes de seção reta triangular, a gente tem que lembrar que o centro de massa a gente acha assim:

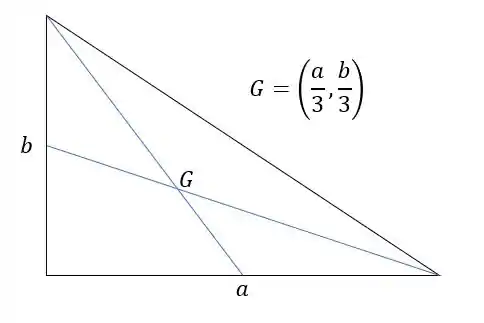
Beleza, então bora lá!

Passo 2

Para o triângulo paralelo ao eixo x , G Δ 1 = 0.5 + 1.5 3 ,   0.25 , 1.8 6 = 1 ,   0.25 ,   0.6 e o volume V Δ 1 = 1 2 ( 0.5 × 1.5 × 1.8 ) ..

Para o retângulo, G r e t = 0.25 ,   1.25 , 1.8 2 = 0.25 ,   1.25 ,   0.9 e o volume V r e t = 0.5 × 2.5 × 1.8 .

Para o outro triangulo, G Δ 2 = 0.25 ,   2.5 + 1.5 3 , 1.8 3 = ( 0.25 ,   3 ,   0.6 ) e o volume V Δ 2 = 1 2 ( 1.8 × 1.5 × 0.5 ) .

Passo 3

Agora é só a gente usar a fórmula do centroide!

x - = ∑ x - V ∑ V = 0.25 0.5 × 2.5 × 1.8 + 0.25 1 2 0.5 × 1.5 × 1.8 + 1 1 2 0.5 × 1.5 × 1.8 0.5 × 2.5 × 1.8 + 1 2 0.5 × 1.5 × 1.8 + 1 2 0.5 × 1.5 × 1.8

x - = 0.391 m

y - = ∑ y - V ∑ V = 1 . 25 0.5 × 2.5 × 1.8 + 3 1 2 0.5 × 1.5 × 1.8 + 0.25 1 2 0.5 × 1.5 × 1.8 0.5 × 2.5 × 1.8 + 1 2 0.5 × 1.5 × 1.8 + 1 2 0.5 × 1.5 × 1.8

y - = 1.39 m

z - = ∑ z - V ∑ V = 0.9 0.5 × 2.5 × 1.8 + 0.6 1 2 0.5 × 1.5 × 1.8 + 0 . 6 1 2 0.5 × 1.5 × 1.8 0.5 × 2.5 × 1.8 + 1 2 0.5 × 1.5 × 1.8 + 1 2 0.5 × 1.5 × 1.8

z - = 0.7875 m

Resposta

x - = 0.391 m

y - = 1.39 m

z - = 0.7875 m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Localize o centroide y da seção transversal da viga.
Uma superfície é gerada girando o arco circular de 0,8 m de raio e ângulo subtendido de 120∘ completamente em torno do eixo z. O diâmetro do pescoço é de 0,6 m. Determine a área externa A gerada.
Calcule as reações de apoio em A e B para a viga carregada.
Calcule a força de apoio RA e o momento MA atuando na viga cantilever carregada em A.
Determine as reações nos apoios A e B para a viga carregada como mostrado.