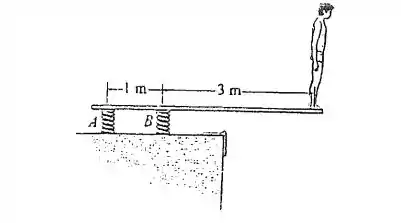
Um homem fica em pé na ponta do trampolim que é sustentado por duas molas A e B, cada uma com rigidez k = 15 kN/m. Na posição mostrada, o trampolim é horizontal. Se o homem possui uma massa de 40 kg , determine o ângulo de inclinação descrito pelo trampolim com a horizontal após ele pular. Despreze o peso do trampolim e considere-o rígido.
Passo 1
Faaala! A gente quer o ângulo que o trampolim faz com a horizontal depois que o jovem ali pula. O que acontece é que quando ele está ali, as molas estão deformadas. Quando ele sai, as molas voltam a sua posição original. Nessa configuração original, o trampolim fica inclinado.
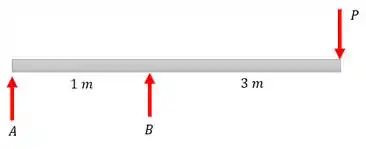
Bem estamos em equilíbrio então as forças verticais, horizontais e momentos binários se anulam
Vamos dar uma olhada no diagrama de forças
Passo 2
Vamos definir uma Orientação antes de começar. Gosto sempre de trabalhar em sentido horário. Essa orientação é arbitrária, se você estiver feito no sentido contrário, beleza! Só ao conferir as contas os sinais estarão trocados.
Então vamos lá. Tudo o que fizer meu sistema tentar rodar em horário é ( + ), tudo o que tentar fazer tentar rodar em sentido contrário é ( - ).
Outra coisa. Quando fazemos momento binário temos que olhar para o PAR distancia e força. Elas têm que ser ortogonais. Show! Vamos cair dentro.
Passo 3
Vamos começar achando as forças em e causadas pelo peso do garoto:
Onde é a gravidade, resolvendo:
Agora o somatório Fy.
E olha só que legal, não há forças em X. E como A está negativo ele aponta na direção contraria a que pensávamos de início.
Passo 4
Pronto! Achamos tudo o que precisamos. Vamos agora pensar o que acontece com o garoto parado. Como a força em está para cima, significa que a mola está lutando para subir, se esticar, então essa mola está comprimida.
Mas como tem uma força para baixo, significa que a mola está querendo muito se encurtar, tanto que puxa o trampolim para baixo, então ela está esticada. Um esqueminha:
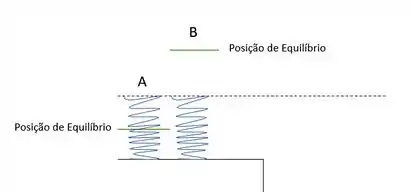
As molas estão fora de sua posição de equilíbrio. A foi esticada e B foi comprimida como resultado do peso do garoto. Retirando esse peso elas vão tentar voltar a sua posição de equilíbrio

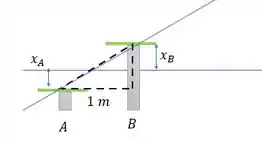
Nisso temos um triangulo com altura ( e base 1 (distância entre A e B)
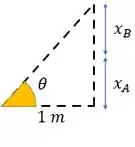
Passo 5
Vamos achar
Vamos achar
Então para achar podemos fazer
Prontinho 😊