Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 6.Problemas - Ex. 96
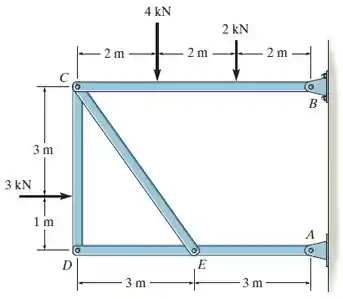
Determine as componentes horizontal e vertical das forças que os pinos em e exercem sobre a estrutura.
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Precisamos determinar as componentes horizontal e vertical das forças que os pinos em e exercem sobre a estrutura.
Nosso primeiro passo será retirar os vínculos nestes pontos e substituir pelas suas forças. Ao fazermos isto, teremos o seguinte diagrama de corpo livre:
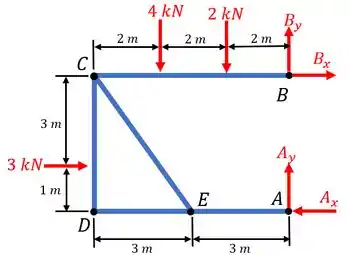
A partir deste diagrama nós já conseguimos calcular duas forças. Para isto, teremos que fazer o somatório dos momentos em torno do ponto e depois do ponto . Obteremos então:
Resolvendo o sistema acima nós obtemos:
Aproveitando este diagrama, vamos obter outra relação que será fundamental no próximo passo. Avaliando o somatório de forças na direção vertical, temos:
Passo 2
Agora vamos analisar apenas o membro . Fazendo o seu diagrama de corpo livre, obtemos:
Podemos obter fazendo o somatório de momentos em torno do ponto , pois assim eliminaremos as reações , e , sendo todas elas incógnitas, da nossa conta. Portanto,
E, para finalizarmos, no final do Passo 1 nós não descobrimos uma relação entre e ? Utilizando-a, vamos obter o seguinte valor de :
E assim finalizamos a questão!