Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 6.Problemas de Revisão - Ex. 6
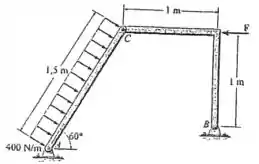
Determine as componentes horizontal e vertical da reação que os pinos e exercem sobre a estrutura de dois membros. Faça .
Passo 1
Para determinar as reações, deve-se fazer o diagrama de corpo livre de cada membro no qual sejam indicadas todas as forças atuando no respectivo membro.
Além disso, é possível fazer uma análise prévia da carga distribuída pelo membro , tal que:
Como a junta está presente em ambos os membros do sistema, pode-se determinar a força exercida sobre essa junta e que estará presente no equilíbrio de forças dos dois membros.
Passo 2
Então, fazendo o DCL do membro e fazendo uma análise de momento em relação ao ponto , tem-se que:
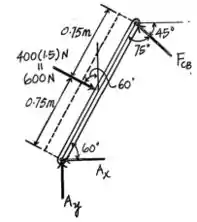
Passo 3
Agora, a partir do valor dessa reação no pino e o DCL do membro é possível determinar as reações em que serão dadas por:
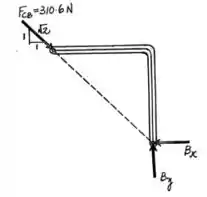
Deve-se observar que o membro juntamente com a linha de ação da reação em forma um triângulo retângulo que possui os dois catetos com a mesma medida. Por esse motivo, ambas as reações em são iguais já que a força será dividida igualmente.
Passo 4
Como agora só faltam as reações em para serem determinadas, é possível fazer o equilíbrio de forças nos eixos e , pois, dessa forma, haverá duas equações para encontrar duas variáveis o que se torna válido.
Então, para o eixo :
E, para o eixo :