Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.3 - Ex. 14

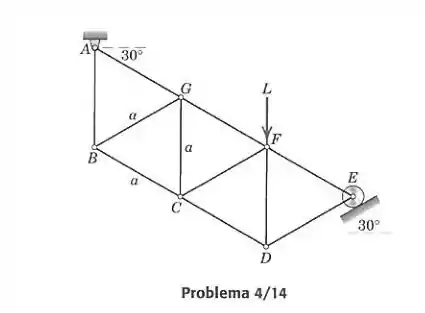
A treliça é formada por triângulos de lado a e está carregada e apoiada como mostrado. Determine as forças nos elementos E F , D E e D F .

Passo 1

Primeiro precisamos resolver as equações de equilíbrio externas ao conjunto, para achar a força do apoio em E . Vamos resolver a equação do momento em torno de A , pois não envolve as forças desconhecidas naquele ponto. A força de apoio em E é normal ao plano de inclinação de 30 ° , então tem uma inclinação em relação à horizontal de 60 ° .

∑ M A = 0 ⇒ - L 2 a cos ⁡ 30 ° + E sen ⁡ 60 ° 3 a cos ⁡ 30 ° - E cos ⁡ 60 ° 3 a sen ⁡ 30 ° = 0  

⇒ - 3 a L + 9 4 a E - 3 4 a E = 0 ⇒ 6 4 E = 3 L ⇒ E = 2 3 3 L

Passo 2

Agora vamos resolver as equações de equilíbrio em x e y   para cada nó. As forças positivas indicam tração e as negativas compressão, e sempre trataremos as forças desconhecidas como tração.

Nó E:

∑ F x = 0 ⇒ - E F cos ⁡ 30 ° - D E cos ⁡ 30 ° - E cos ⁡ 60 ° = 0

⇒ - 3 2 E F + D E = 3 3 L ⇒ E F + D E = - 2 3 ⋅ 3 3 L

⇒ E F + D E = - 2 3 L       ( 1 )

∑ F y = 0 ⇒ E F sen ⁡ 30 ° - D E sen ⁡ 30 ° + E s e n   60 ° = 0

⇒ 1 2 E F - D E + 3 2 E = 0

Substituindo o valor de E :

1 2 E F - D E = - 2 3 3 L ⋅ 3 2 = - L ⇒ E F - D E = - 2 L         ( 2 )

Somando as (1) e (2):

E F + D E + E F - D E = - 2 3 L - 2 L

2 E F = - 8 3 L ⇒ E F = - 4 3 L   ( C )

Agora voltamos em (1) para encontrar D E :

D E = - 2 3 L + 4 3 L ⇒ D E = 2 3 L   ( T )

Passo 3

Nó D:

∑ F x = 0 ⇒ - C D cos ⁡ 30 ° + D E cos ⁡ 30 ° = 0

Dividimos tudo por cos ⁡ 30 ° :

⇒ - C D + D E = 0 ⇒ C D = D E = 2 3 L   ( T )

∑ F y = 0 ⇒ C D sen ⁡ 30 ° + D E sen ⁡ 30 ° + D F = 0

Substituindo sen ⁡ 30 ° = 1 2 e os valores de C D e D E :

⇒ 2 3 L 1 2 + 2 3 L 1 2 + D F = 0 ⇒ D F = - 2 3 L   ( C )

Resposta

E F = - 4 3 L   ( C )

D E = 2 3 L   ( T )

D F = - 2 3 L   ( C )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a força desenvolvida em cada membro da treliça espacial e indique se os membros estão sob tração ou compressão. A caixa possui um peso de 750N .
Determine a força nos membros F E e E D da treliça espacial e indique se os membros estão sob tração ou compressão. A treliça é sustentada por juntas esféricas em C e ligações curtas em A e B .
Determine a força nos membros B E , D F e B C da treliça espacial e indique se os membros estão sob tração ou compressão.
Determine a força nos membros A B , A E , B C , B F , B D e B E da treliça de espaço e indique se os membros estão sob tração ou compressão.
Determine a força nos membros A B , C D , E D e C F da treliça espacial e indique se os membros estão sob tração ou compressão.