Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.3 - Ex. 15

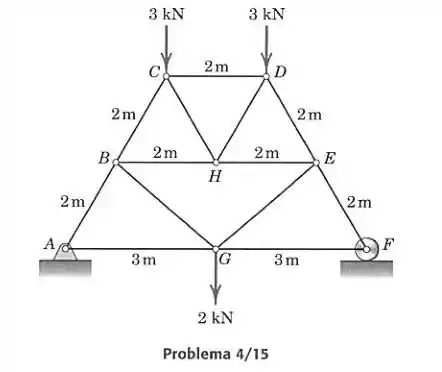
Determine as forças nos elementos B C e B G da treliça carregada.

Passo 1

Primeiro devemos calcular as forças externas aplicadas na treliça em A e F . Esses apoios devem anular as forças aplicadas, em C , D e G , então, pela simetria, os dois aplicam uma mesma força pa cima:

A = F = 3 + 3 + 2 2 = 4   k N

Não há forças aplicadas na horizontal por conta do formato do apoio em F .

Passo 2

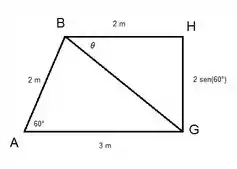
Agora devemos resolver as equações de equilíbrio em x e y   para cada nó, mas antes precisamos do valor dos ângulos que usaremos nos cálculos. Os ângulos B A ^ G = C B ^ H são iguais a 60 ° . Agora, o ângulo θ = H B ^ G :

B G - = 2 2 + 2 ⋅ 3 2 2 = 7

⇒ sen ⁡ θ = 3 7   e cos ⁡ θ = 2 7

Passo 3

Nas equações de equilíbrio dos nós, as forças positivas indicam tração e as negativas compressão, e sempre trataremos as forças desconhecidas como tração.

Nó A:

∑ F x = 0 ⇒ A B cos ⁡ 60 ° + A G = 0 ⇒ A G = - A B 2

∑ F y = 0 ⇒ A B sen ⁡ 60 ° + 4 = 0 ⇒ 3 2 A B = - 4 ⇒ A B = - 8 3   k N   ( C )

⇒ A G = 4 3   k N   ( T )

Por simetria, também obtemos:

F G = 4 3   k N   ( T )

E F = - 8 3   k N   ( C )

Passo 4

Nó D:

Por simetria, temos B G = E G .

∑ F y = 0 ⇒ B G sen ⁡ θ + E G sen ⁡ θ - 2 = 0 ⇒ 2 B G sen ⁡ θ = 2 ⇒ B G = E G = 7 3   k N   ( T )

Passo 5

Nó (C):

∑ F y = 0 ⇒ - A B sen ⁡ 60 ° + B C sen ⁡ 60 ° - B G sen ⁡ θ = 0 ⇒ 8 3 ⋅ 3 2 + 3 2 B C - 7 3 ⋅ 3 7 = 0

⇒ 3 2 B C = - 3 ⇒ B C = - 2 3   k N   ( C )

Resposta

B C = 2 3   k N = 3,46   k N   ( C )

B G = 7 3   k N = 1,53   k N   ( T )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se cada membro da treliça espacial pode sustentar uma força máxima de 600N sob compressão e 800N sob tração, determine a maior força F que a treliça pode sustentar.
Determine a força nos membros E F , D F , C F e C D da treliça espacial e indique se os membros estão sob tração ou compressão.
Determine as componentes horizontal e vertical da reação no pino C .
Determine a força em cada membro da treliça e indique se os membros estão sob tração ou compressão.
A treliça usada para sustentar um balcão está sujeita às cargas mostradas. Considere cada nó como um pino e determine a força em cada membro. Indique se os membros estão sob tração ou compressão. Faça