Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.3 - Ex. 12
Cada elemento da treliça é uma barra uniforme de 8 m pesando 400 kg. Calcule a tração ou compressão média em cada elemento, devida aos pesos dos elementos.
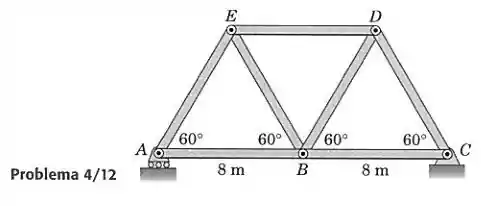
Passo 1
Primeiro vamos determinar as forças externas em e que atuam na treliça. Com , sabemos que o peso total da treliça é:
O apoio em apenas causa força vertical. Por simetria, então, os apoios em e fazem força para cima, cada um aplicando uma carga de .
Passo 2
Vamos agora calcular as equações de equilíbrio para cada nó. indica que o elemento está comprimido e indica que ele está tracionado. Consideraremos todas as forças desconhecidas de tração, e se obtivermos um valor negativo quer dizer que são de compressão.
Nó A:
Por simetria entre os elementos, obtemos também:
Passo 3
Nó E:
Por simetria:
Resposta
Exercícios de Livros Relacionados
6.21 Determine a maior massa m do bloco suspenso de modo que a força em qualquer membro da treliça não exceda 30k N( T ) ou 25k N( C )
6.22 Determine a força em cada membro da treliça e indique se os membros estão sobre tração ou compressão.
6.7 Determine a força nos membros BC, CF e FE. Indique se os membros estão sob tração ou compressão.
6.8 Determine a força nos membros LK, KC e CD da treliça. Indique se os membros estão sob tração ou compressão.
Determine a força em cada membro da treliça. Indique se os membros estão sob tração ou compressão.