Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 5.Problemas de Revisão - Ex. 7
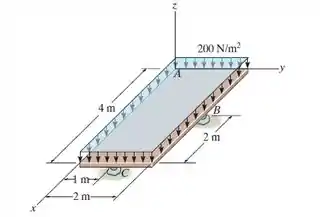
Determine as componentes , , das reações nos suportes de esfera e e na junta esférica (não mostrada) para a placa uniformemente carregada.
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Esta é uma questão bem tranquila. Precisamos descobrir as reações em cada um dos suportes.
Como os suportes e são esferas, elas possuem reação vertical apenas. Já o suporte em pode possuir reação nas três direções!
A chave para resolvermos esta questão está nas equações de equilíbrio (somatório de momentos e somatório de forças igual a zero).
Mas, para que a gente consiga aplicar esta relação, vamos substituir o carregamento distribuído por uma força pontual. Esta força terá intensidade:
E será aplicada para baixo no ponto médio da placa.
Agora que a gente já sabe o que fazer, vamos as contas!
Passo 2
Agora é a hora de aplicarmos as equações de equilíbrio. Vamos começar fazendo o somatório de momentos em torno do ponto . Portanto,
Das duas primeiras equações nós conseguimos obter que .
Já da terceira equação não conseguimos extrair nenhuma informação ainda. Portanto, vamos guardá-la para trabalhar posteriormente.
Passo 3
Agora vamos fazer o somatório de momentos em torno do ponto . Portanto,
Das duas primeiras equações obtemos que .
Novamente, não conseguimos extrair nenhuma informação da terceira equação ainda. Portanto, vamos guardá-la para trabalhar posteriormente.
Passo 4
Para finalizarmos a questão nós temos que descobrir quem são as reações e .
Mas da onde iremos conseguir estas equações??? Diretamente do somatório de forças na direção e direção ! Estas equações são:
E assim nós finalizamos a questão!