Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 75
Determine os componentes de todas as forças que atuam em cada membro da estrutura carregada.
Passo 1
Fala galera, tudo certo? Bora fazer mais um exercício? Prometo que vai ser bem rapidinho!
O enunciado nos pede para determinar as componentes de todas as forças que atuam nos elementos, devido aos dois carregamentos na estrutura.
Show, então bora lá! Antes de resolver, vamos fazer o diagrama de corpo livre para entendermos melhor o problema.
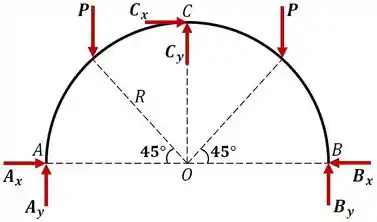
Passo 2
Bom, para que a estrutura esteja em equilíbrio, o ponto também deve estar. Sendo assim, vamos analisar separadamente os membros e do arco, que são totalmente simétricos. Quando aplicamos a força , ela empurra o ponto para baixo em ambos os membros com a mesma intensidade. Vamos chamar de a força no arco e de a força no arco .
Por outro lado, como na verdade esses membros estão conectados, quando o membro força para baixo, ele responde forçando para cima. Da mesma forma quando empurra para baixo, ele responde forçando para cima.
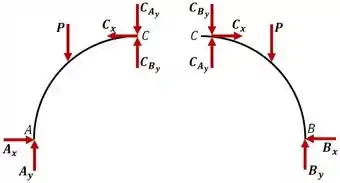
Uma vez que e são de mesma intensidade e com sentidos contrários em cada membro, eles se anulam o que resulta em:
Passo 3
Tranquilinho né? Agora que já sabemos que vamos analisar como ficam as configurações dos arcos e :
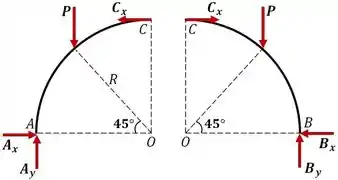
Lembrando que eles são totalmente simétricos, então vamos fazer os cálculos para o lado e os resultados valem para o labo , ou seja:
Passo 4
Como a estrutura está em equilíbrio, os semiarcos também devem estar. Utilizando então o somatório de forças na direção vertical, temos:
Para encontrar , vamos usar o equilíbrio de momentos em torno de :
E, finalmente:
Esse foi tranquilo né? Muitos exercícios são mais de análise do que cálculo em si.
Agora, partiu pra próxima!
HYPERLINK "https://emojiterra.com/pt/rosto-piscando/" 