Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 80
Determine a força de corte exercida na haste em termos das forças aplicadas nos cabos da fresa de alta resistência.
Passo 1
Fala galera, tudo certo? Bora fazer mais um exercício? Prometo que vai ser bem rapidinho!
O enunciado nos pede para determinar a força na haste em devido aos carregamentos aplicados em e .
Show, então bora lá! Para começar, vamos analisar o membro e as forças que atuam nele.
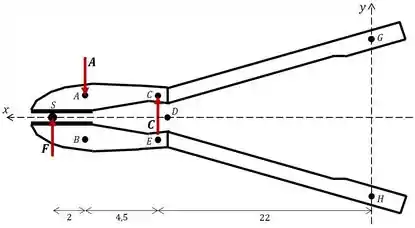
Sabemos que a força de reação que a haste exerce na peça , é igual à força de corte exercida na própria haste. Uma vez que a reta que liga é vertical, a força exercida pela parte no pino (força ) também é vertical, portanto, a força de reação no pino também deve ser vertical (não há forças com componente horizontal sendo aplicadas).
Show! Vamos utilizar então o equilíbrio de momentos em torno de para descobrir a força de reação do sistema em função dessa força de corte :
Passo 2
Tranquilinho né? Agora vamos analisar o outro lado da peça, o cabo onde é aplicada a força em .
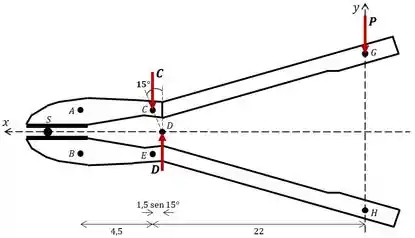
De forma similar, vamos fazer o equilíbrio de momentos em torno do ponto para expressar a reação em em função da força aplicada.
Show de bola! Observe que a gente utilizou a equação de equilíbrio de momentos duas vezes para as duas peças que compõem a fresa de alta resistência. Podemos fazer isso porque a estrutura como um todo deve estar em equilíbrio.
Passo 3
Agora ficou fácil determinar a força de corte em função das forças aplicadas em e , pois o ponto que encontramos em função dessas duas forças ( e ) é o mesmo. Sendo assim, podemos igualar os resultados obtidos nos passos 1 e 2 e isolar em função de :
Sim gente, só isso!! Da pra acreditar?
Agora partiu pra próxima!
HYPERLINK "https://emojiterra.com/pt/rosto-piscando/" 